Faculty of Applied Physics and Mathematics

Programowanie w SAS, Matematyka Finansowa, semestr 4 WFTiMS

Orientacyjny program wykładu:

Wykład:

• Wprowadzenie:

1)      Właściwości optyczne materiałów: współczynnik absorpcji, załamania i odbicia;

2)      Generacja i rekombinacja nośników ładunku w półprzewodniku;

3)      Zjawisko fotoelektryczne wewnętrzne;

• Zasada działania ogniwa fotowoltaicznego:

1)      Zjawiska;

2)      Efektywność konwersji energii;

3)      Czynniki wpływające na efektywność konwersji energii;

• Konstrukcja ogniwa fotowoltaicznego, stosowane materiały i rozwiązania na przykładzie ogniwa krzemowego:

1)      Emiter i baza;

2)      Warstwy antyodbiciowe;

3)      Elektrody;

4)      Ogniwa cienkowarstwowe z amorficznego krzemu;

• Inne materiały i technologie:

1)      Ogniwa cienkowarstwowe CdTe, CIGS, ogniwa perowskitowe;

2)      Ogniwa fotoelektrochemiczne, bioogniwa;

3)      Ogniwa wielozłączowe;

4)      Skupianie światła;

• Panele słoneczne:

1)      Materiały i rozwiązania stosowane w panelach;

2)      Zastosowanie paneli;

3)      Porównanie różnych technologii;

• Inne urządzenia wykorzystujące zjawisko fotoelektryczne wewnętrzne (fotorezystory, fotodiody) oraz materiały i technologie stosoane do ich wytwarzania.
• Podsumowanie i przedstawienie najnowszych materiałów, rozwiązań technicznych itp. w zakresie fotowoltaiki

Seminarium: Dyskusja pomiędzy studentami na temat zagadnień związanych ze stosowaniem ogniw fotowoltaicznych, opłacalnością ich stosowania, prognozami na przyszłość oraz problemami związanymi z ich recyklingiem

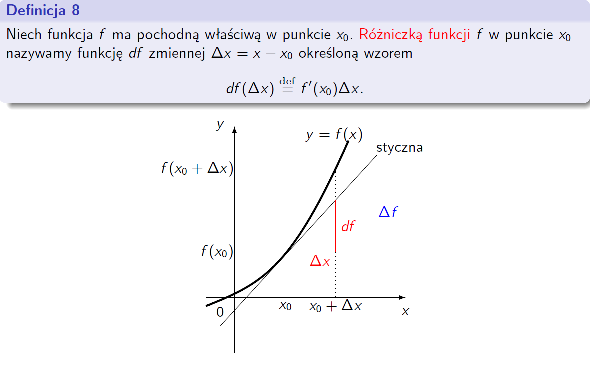
Kurs zawiera materiały do wykładów i ćwiczeń z Analizy Matematycznej dla studentów kierunków Fizyka Techniczna i Podstawy Nauk Technicznych (semestr 1 i 2) na WFTiMS.

Kurs dotyczy bioinformatyki. Bioinformatyka jest dziedziną nauki, w
której biologia, informatyka oraz technologie informacyjne zlewają się w
jedną dyscyplinę.

Ćwiczenia, Chemia II, kierunek Nanotechnologia Ist, sem.II, grupa I

Dielectric materials - properties, applications, structure.