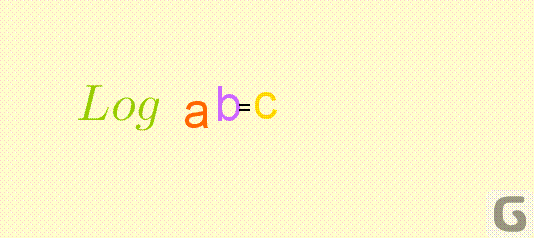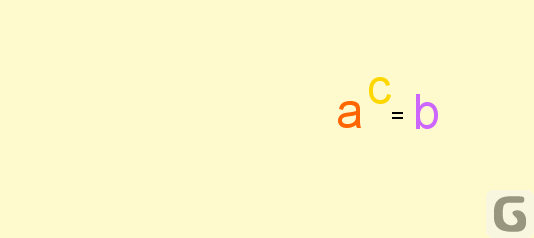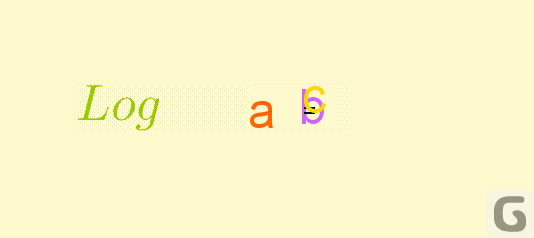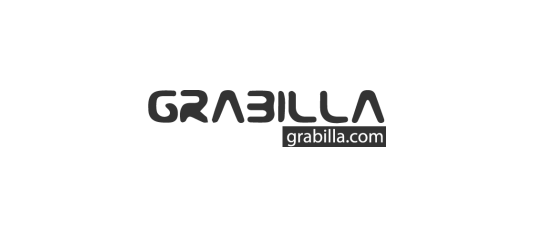Logarytm - definicja i własności

Niech \(a\), \(x\) będą dodatnimi liczbami rzeczywistymi oraz niech \(a\neq 1\). 

Wtedy logarytm o podstawie \(a\) z \(x\) jest to liczba \(c\) taka, że:

\(\log_ a{x} = c \quad\) wtedy i tylko wtedy, gdy \(\quad a ^ c= x\)

W powyższym zapisie \(a\) nazywamy podstawą logarytmu, podczas gdy zmienna \(x\) jest nazywana argumentem logarytmu.

Oznaczenia, które zostały przedstawione powyżej, są modyfikowane dla logarytmów o dwóch wyróżnionych podstawach:

• Dla \(a=e\) (określenie i definicję liczby \(e\) znajdziesz tutaj) przyjmuje się oznaczenie:

\(\log_e{x}=\ln{x}\)

logarytm o podstawie \(e\) nazywamy logarytmem naturalnym.

• Dla \(a=10\) funkcjonuje oznaczenie:

\(\log_{10}{x}=\log{x}\)

Logarytm o podstawie \(10\) nosi nazwę logarytmu dziesiętnego.

Z jakiego powodu w powyższej definicji logarytmu zakłada się, że \(a\neq 1\)?

Gdyby \(a\) było równe \(1\), to:

• dla \(x\neq 1\) logarytm \(log_{a}{x}\) by nie istniał.
• dla \(x=1\) logarytm \(log_{a}{x}\) nie byłby jednoznaczne określony.

\(a^{\log_a{b}}=b\)

Stosują definicję logarytmu dla oczywistej równości \(\log_a{b}=\log_a{b}\) otrzymujemy, że \(a^{\log_a{b}}=b\) (\(\log_a{b}=c \) wtedy i tylko wtedy, gdy \( a^c=b\), za \(c\) podstawiamy \(\log_a{b}\)).

Przykłady

\(3^{\log_3{2}}=2\)

\(2^{\log_2{3}}=3\) 

\(log_a{b^p}=p\cdot log_a{b}\) 

Zgodnie z definicją logarytmu \(\log_a{b^p}=p\log_a{b}\) wtedy i tylko wtedy, gdy \(a^{p\log_a{b}}=b^p\). Ale \(a^{p\cdot \log_a{b}}=(a^{\log_a{b}})^p=b^p\). Skorzystaliśmy tutaj z własności 1.

Przykłady

\(\log_2{9}=\log_2{3^2}=2\cdot \log_2{3}\)

\(3\cdot \log_3{2}=\log_3{2^3}=\log_3{8}\)

\(\log_{a^p}b=\frac{1}{p}\log_a{b}\)

Mamy, że \(\log_{a^p}b = \frac{1}{p}\log_a{b}\) wtedy i tylko wtedy, gdy \((a^p)^{\frac{1}{p}\log_a{b}}=b\). Jest to spełnione, gdyż \((a^p)^{\frac{1}{p}\log_a{b}}=a^{p\cdot \frac{1}{p}\log_a{b}}=a^{\log_a{b}}=b\). Skorzystaliśmy z własności 1 oraz własności potęg.

Przykłady

\(\log_8{3}=\log_{2^3}3=\frac{1}{3}\log_2{3}\)

\(\frac{1}{2}\log_3{5}=\log_{3^2}5=\log_9{5}\)

\(\log_a{b}+\log_a{c}=\log_a{bc}\) 

Zgodnie z definicją logarytmu \(\log_a(bc)=\log_a{b}+\log_a{c}\) wtedy i tylko wtedy, gdy \(a^{\log_a{b}+\log_a{c}}=bc\). Jest to prawdą, gdyż \(a^{\log_a{b}+\log_a{c}}=a^{\log_a{b}}\cdot a^{\log_a{c}}=bc\). Skorzystaliśmy z własności 1 oraz własności potęg.

Przykłady

\(\log{2}+\log{5}=\log{2\cdot 5}=\log{10}=1 \) (bo \(10^1=10\))

\(\log_2{6}=\log_2(2\cdot 3)=\log_2{2}+\log_2{3}=1+\log_2{3}\)

\(\log_a{b}-\log_a{c}=\log_a{\frac{b}{c}}\)

Zgodnie z definicją logarytmów \(\log_a{\frac{b}{c}}=\log_a{b}-\log_a{c}\) wtedy i tylko wtedy, gdy \(a^{\log_a{b}-\log_a{c}}=\frac{b}{c}\). Jest to spełnione, gdyż \(a^{\log_a{b}-\log_a{c}}=\frac{\log_a{b}}{\log_a{c}}=\frac{b}{c}\). Skorzystaliśmy z własności 1 oraz własności potęg.

Dowód ten można też przeprowadzić inaczej: \(\log_a{b}-\log_a{c}=\log_a{b}+(-\log_a{c})=\log_a{b}+\log_a{c^{-1}}=\log_a(b\cdot c^{-1})=\log_a{\frac{b}{c}}\). Skorzystaliśmy tu z własności 2 i 4.

Przykłady

\(\log_5{10}-\log_5{2}=\log_5{\frac{10}{2}}=\log_5{5}=1\)

\(\log_2{\frac{8}{3}}=\log_2{8}-\log_2{3}=3-\log_2{3}\)

\(\log_a{b}=\frac{\log_c{b}}{\log_c{a}}\)

\(\log_a{b}=\frac{\log_c{b}}{\log_c{a}}\) wtedy i tylko wtedy, gdy \(\log_a{b}\cdot \log_c{a}=\log_a{b}\), co zgodnie z definicją logarytmu oznacza, że \(c^{\log_a{b}\cdot \log_c{a}}=b\). Ale \(c^{\log_a{b}\cdot \log_c{a}}=(c^{\log_c{a}})^{\log_a{b}}=a^{\log_a{b}}=b\) czyli równość jest spełniona. Skorzystaliśmy z własności 1 oraz własności potęg.

Przykłady

\(\log_{\sqrt{2}}\sqrt[3]{2}=\frac{\log_2{\sqrt[3]{2}}}{\log_2{\sqrt{2}}}=\frac{\log_2{2^{\frac{1}{3}}}}{\log_2{2^{\frac{1}{2}}}}=\frac{\frac{1}{3}}{\frac{1}{2}}=\frac{2}{3}\)

\(\log_{\sqrt[3]{3}}{\sqrt{3}}=\frac{\log_3{\sqrt{3}}}{\log_3{\sqrt[3]{3}}}=\frac{\log_3{3^{\frac{1}{2}}}}{\log_3{3^{\frac{1}{3}}}}=\frac{\frac{1}{2}}{\frac{1}{3}}=\frac{3}{2}\)

Dowód opiera się na własności 6: \(\log_a{b}=\frac{\log_b{b}}{\log_b{a}}=\frac{1}{\log_b{a}}\).

Przykłady

\(\log_{2\sqrt{2}}{2}=\frac{1}{\log_2{2\sqrt{2}}}=\frac{1}{\log_2{2}+\log_2{\sqrt{2}}}=\frac{1}{1+\frac{1}{2}}=\frac{1}{\frac{3}{2}}=\frac{2}{3}\)

\(\log_{3\cdot \sqrt[3]{3}}{3}=\frac{1}{\log_3(3\cdot \sqrt[3]{3})}=\frac{1}{\log_3{3}+\log_3{\sqrt[3]{3}}}=\frac{1}{1+\frac{1}{3}}=\frac{1}{\frac{4}{3}}=\frac{3}{4}\)

\(a^{\log_b{c}}=c^{\log_b{a}}\)

Obłóżmy obie strony wywodzonej równości logarytmem o podstawie \(b\).

\(\log_b{(a^{\log_b{c}})}=\log_b{(c^{\log_b{a}})}\)

Korzystając teraz z własności 2 otrzymujemy:

\(\log_b{c}\cdot \log_b{a}=\log_b{a}\cdot \log_b{c}\)

ostatnia tożsamość dowodzi prawdziwości własności 8.

Przykład

\(10^{\ln_2}\cdot 2^{\ln{10}}=10^{\ln{2}}\cdot 2^{\ln{10^{-1}}}=10^{\ln{2}}\cdot 2^{-\ln{10}}=10^{\ln{2}}\cdot (2^{\ln{10}})^{-1}=10^{\ln{2}}\cdot (10^{\ln{2}})^{-1}=1\)