Funkcje wykładnicze i logarytmiczne.
Funkcje wykładnicze i logarytmiczne.
Funkcja wykładnicza
Funkcja wykładnicza jest funkcją postaci:
\(f(x)=a^x\),
gdzie \(a\) jest ustaloną stałą dodatnią różną od \(1\) zaś \(x\) dowolną liczbą rzeczywistą.
Z powyższej definicji wynika, że dziedziną funkcji wykładniczej jest cały zbiór liczb rzeczywistych \(\mathbb R\).
Zapamiętaj - to jest ważne
Funkcji wykładniczej nie należy mylić z funkcją potęgową, która w odróżnieniu od pierwszej wyraża się wzorem:
\(f(x)=x^a\).
Poniższa animacja pokazuje kształt wykresu funkcji wykładniczych w zależności od parametru \(a\).
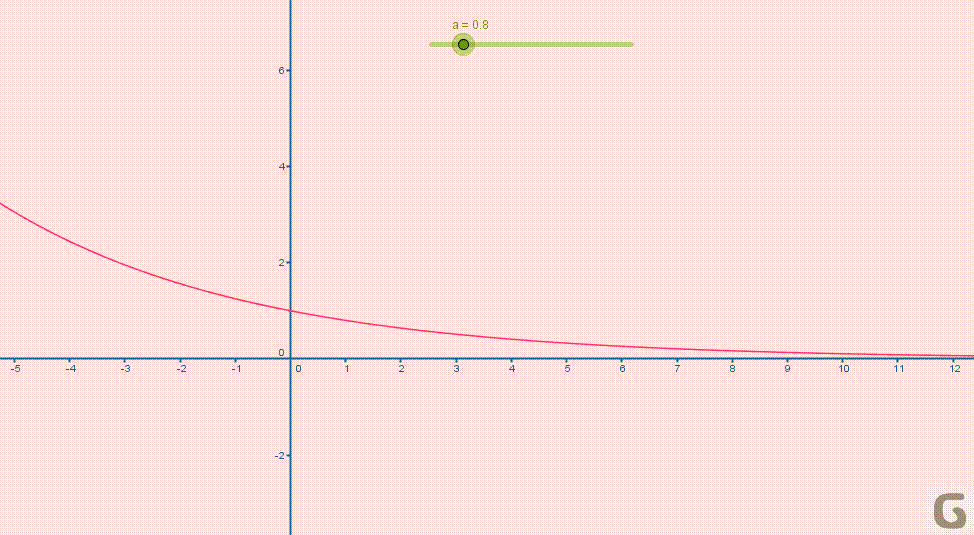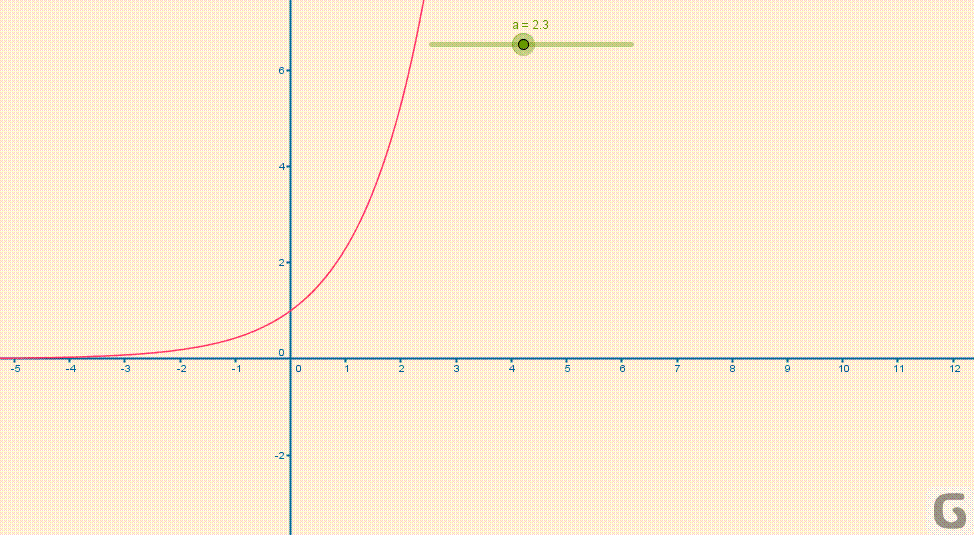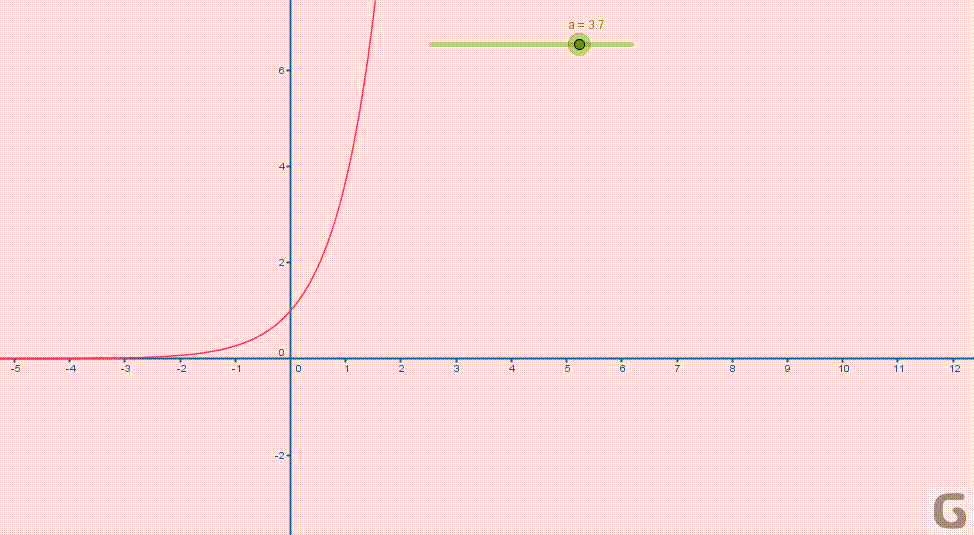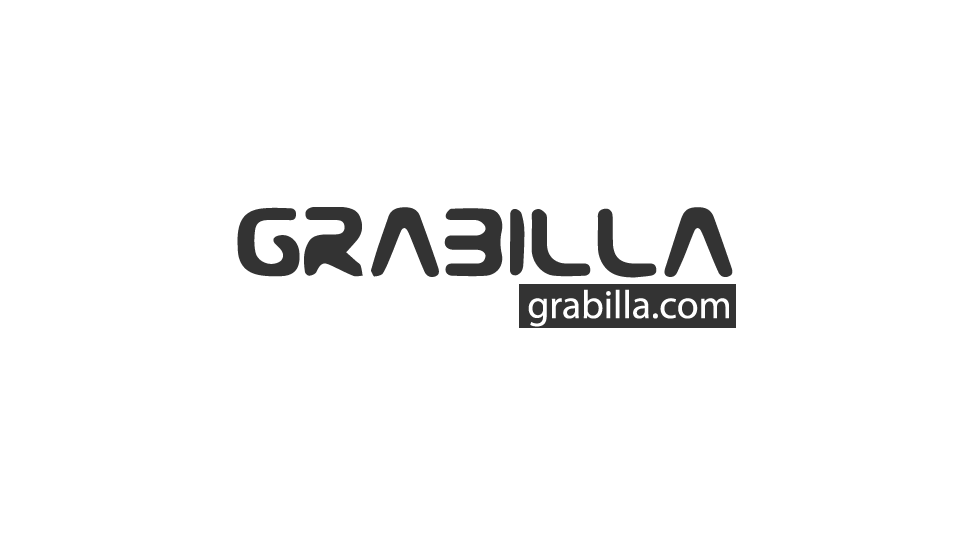
Z uwagi na szereg własności związanych m.in. z rachunkiem różniczkowym, całkowym i analizą zespoloną własną nazwą została wyróżniona funkcja wykładnicza o podstawie \(e\).
Nazewnictwo
Funkcję \(e^x\) określamy nazwą funkcji eksponencjalnej.
Własności funkcji wykładniczych.
-
Zbiór wartości
Zbiorem wartości funkcji wykładniczej jest \(\mathbb R_+\). (w szczególności funkcja \(a^x\) osiąga tylko i wyłącznie wartości dodatnie.)
-
Funkcja wykładnicza jest różnowartościowa.
Powyższy fakt ma szerokie zastosowania dla rozwiązywania równań wykładniczych.
Formalnie wyraża się on zależnością:
\(a^x=a^y\) wtedy i tylko wtedy, gdy \(x=y\),
gdzie \(a\) jest różną od \(1\) stałą dodatnią, a \(x, y\) dowolnymi liczbami rzeczywistymi.
-
Monotoniczność
- dla \(a\in(0,1)\) funkcja \(y = a^x\) jest malejąca co oznacza, że \(a^x<a^y\) wtedy i tylko wtedy, gdy \(x>y\)
- dla \(a>1\) funkcja \(y = a^x\) jest rosnąca co oznacza, że \(a^x<a^y\) wtedy i tylko wtedy, gdy \(x<y\)
Zadanie do przemyślenia
W definicji funkcji wykładniczej zastrzegliśmy, że jej podstawa musi być różna od \(1\). Zastanów się, które z powyższych własności uległyby zmianie dla hipotetycznie rozważonej tu funkcji \(y = 1^x\).
Kolejne własności są związane z pojęciem granicy funkcji. Jako, że nie każdy użytkownik kursu zdążył zaznajomić się z tematyką granic funkcji, lektura tej części strony nie jest konieczna dla ukończenia kursu. Poniższe własności funkcji wykładniczej są tu jednak prezentowane z uwagi na ich duże zastosowanie w rozwiązywaniu zadań związanych z dalszymi tematami kursu matematyki.
Materiały dodatkowe
Niech \(a\in(0,1)\). Wtedy:
\(\lim_{x\to\infty} a^x = 0\) oraz \(\lim_{x\to-\infty}a^x=\infty\).
Niech \(a>1\). Wtedy:
\(\lim_{x\to\infty} a^x = \infty\) oraz \(\lim_{x\to-\infty}a^x= 0\)
Ponadto dla dowolnego \(a\in\mathbb R_+\setminus\{1\}\) prosta \(y=0\) jest asymptotą poziomą funkcji \(y = a^x\) i jest to jej jedyna asymptota.
Funkcja logarytmiczna
Funkcja logarytmiczna jest funkcją postaci:
\(f(x)=\log_a{x}\),
gdzie \(a\) jest ustaloną stałą dodatnią różną od \(1\) zaś \(x\) dowolną liczbą rzeczywistą dodatnią.
Z powyższej definicji wynika, że dziedziną funkcji logarytmicznej jest zbiór liczb rzeczywistych dodatnich \(\mathbb R_+\) (oznacza to, że funkcję logarytmiczną możemy rozpatrywać jedynie dla argumentów dodatnich).
Funkcja logarytmiczna jest funkcją odwrotną do funkcji wykładniczej.
Graficznie powyższa zależność jest zilustrowana (po wyborze w menu rozwijalnym opcji Funkcje logarytmiczne -logarytm naturalny) tutaj.
Formalnie, fakt że funkcje logarytmiczne i wykładnicze są wzajemnie odwrotne wyraża się równoważnością:
\(a ^ { x } = c\) wtedy i tylko wtedy, gdy \(\log_a{c} = x\)
Podobnie jak w przypadku funkcji wykładniczej, o stałej \(a\) zakładamy tu, że jest liczbą dodatnią różną od \(1\).
Kształt wykresu funkcji logarytmicznej w zależności od podstawy \(a\) przedstawia poniższa animacja:
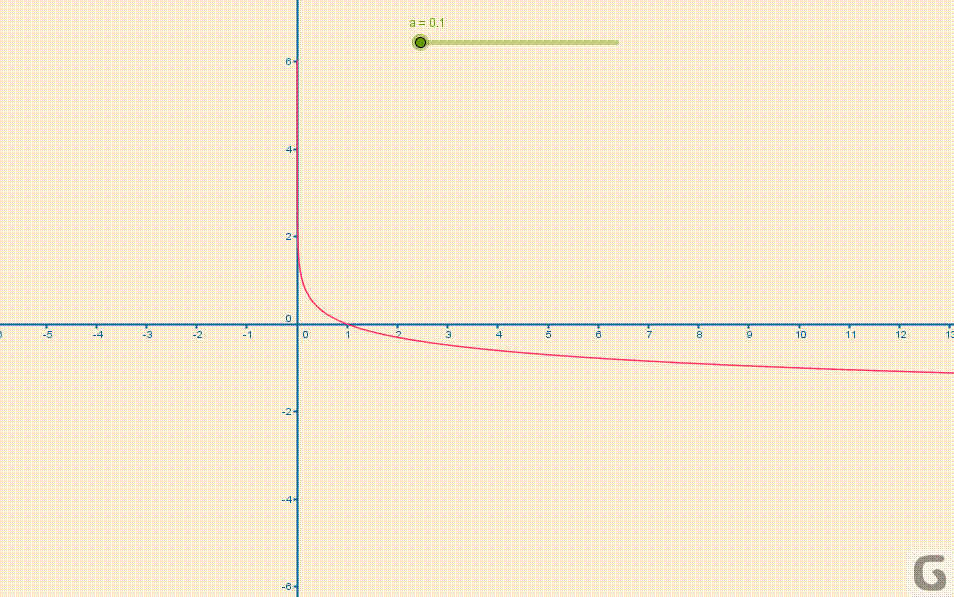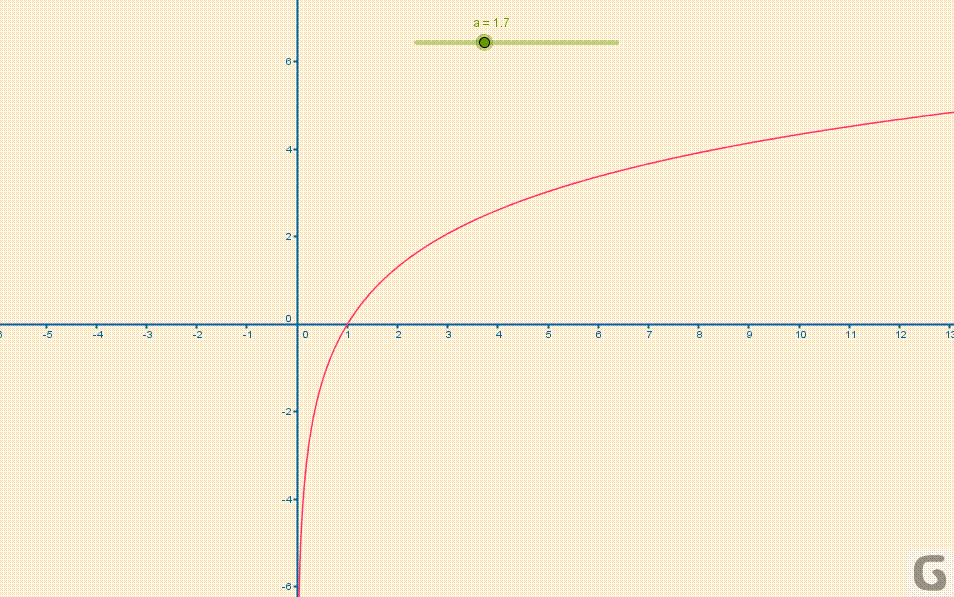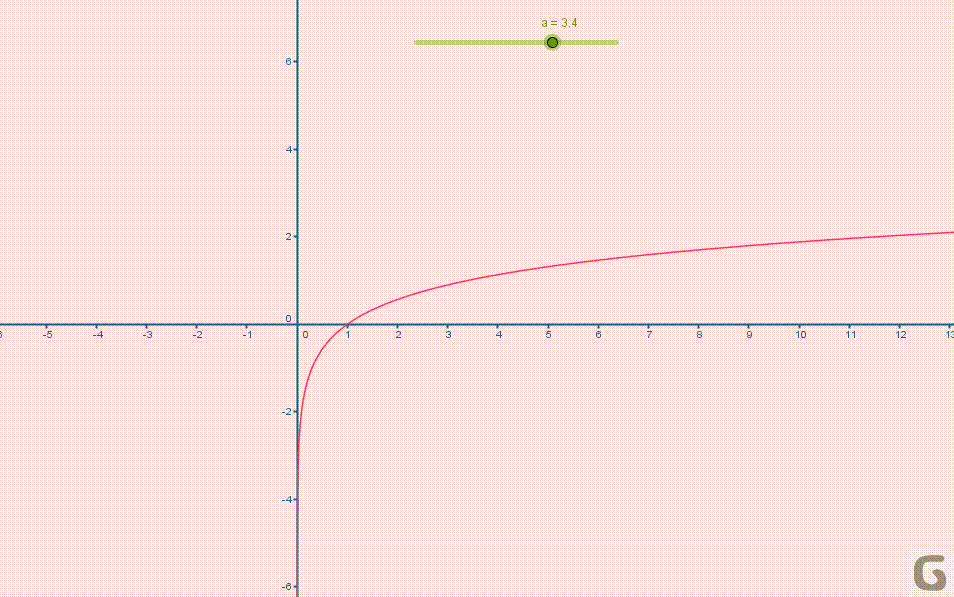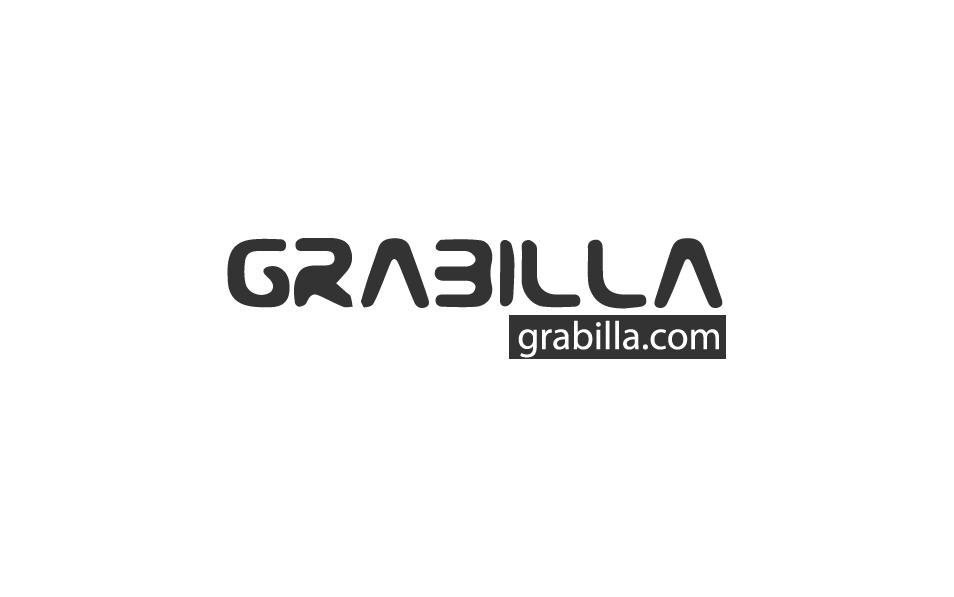
Własności funkcji logarytmicznej.
Jak widać na załączonej animacji wykres funkcji odwrotnej (logarytmicznej) jest symetryczny względem prostej \(y=x\) do wykresu funkcji wyjściowej (wykładniczej). Wynika z tego, że dziedzina tej pierwszej jest równa przeciwdziedzinie drugiej i odwrotnie.
-
Zbiór wartości
Zbiorem wartości funkcji logarytmicznej jest zbiór \(\mathbb R\).
Operacja odwracania funkcji zachowuje monotoniczność. Oznacza to, że funkcja odwrotna do funkcji rosnącej jest funkcją rosnącą, funkcja odwrotna do funkcji malejącej jest malejąca. Każda funkcja odwracalna jest ponadto funkcją różnowartościową. Fakty te, zebrane razem, decydują o tym, że kolejne własności są w bezpośredni sposób analogiczne do podobnych dla funkcji wykładniczej.
-
Funkcja logarytmiczna jest różnowartościowa
Ta własność również znajdzie szerokie zastosowania dla rozwiązywania równań logarytmicznych.
Oznacza ona bowiem, że w równaniach, w których obie strony są logarytmami przy tej samej podstawie można pomijać logarytm, przyrównując do siebie jedynie jego argumenty.
-
Monotoniczność
- dla \(a\in(0,1)\) funkcja \(y = \log_a{x}\) jest malejąca, co oznacza, że \(\log_a{x}<\log_a{y}\) wtedy i tylko wtedy, gdy \(x>y\).
- dla \(a>1\) funkcja \(y = \log_a{x}\) jest rosnąca, co oznacza, że \(\log_a{x}<\log_a{y}\) wtedy i tylko wtedy, gdy \(x<y\).
Zestawienie faktów dotyczących funkcji logarytmicznej również uzupełnimy wzmianką o jej zachowaniu na krańcach przedziału określoności.
Materiały dodatkowe
Niech \(a\in(0,1)\). Wtedy:
\(\lim_{x\to\infty} \log_a{x}= -\infty\) oraz \(\lim_{x\to 0^+} \log_a{x}=\infty\).
Niech \(a>1\). Wtedy:
\(\lim_{x\to\infty} \log_a{x}= \infty\) oraz \(\lim_{x\to 0^+} \log_a{x}=-\infty\)
Ponadto dla dowolnego \(a\in\mathbb R_+\setminus\{1\}\) prosta \(x=0\) jest asymptotą pionową prawostronną funkcji \(y = \log_a{x}\) i jest to jedyna jej asymptota.