Podstawowe definicje i własności
Podstawowe definicje i własności
Definicja
Liczbą zespoloną nazywamy uporządkowaną parę liczb rzeczywistych, np. \((x,y)\). Liczby zespolone oznaczamy przez \(z\), a zbiór wszystkich liczb zespolonych przez \(\mathbb{C}\).
Mamy zatem
\(\color{red}{\mathbb{C}=\{z=(x,y)\;,\;\;\;x,\;y\in \mathbb{R}\}}\;\).
Liczbę zespoloną \(z\) przedstawiamy na płaszczyźnie w postaci punktu o współrzędnych \((x,y)\) lub w postaci wektora o początku w punkcie \((0,0)\) i końcu w punkcie \((x,y)\). Zbiór wszystkich liczb zespolonych w tej interpretacji nazywamy płaszczyzną zespoloną.
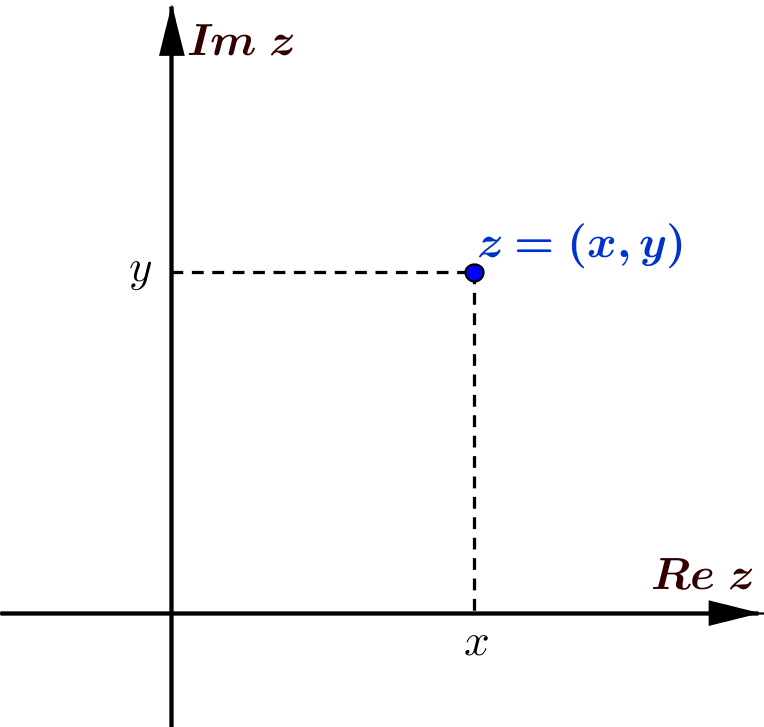
Na rysunku \(Re\;z \;\) jest to tak zwana oś rzeczywista, a \(Im \;z \;\) oś urojona.
Definicja
Niech \(z_1=(x_1,y_1)\), \(z_2=(x_2,y_2)\) będą liczbami zespolonymi. Wtedy
- \(z_1=z_2 \Leftrightarrow (\;x_1=x_2\;\wedge\;y_1=y_2\;)\);
- \(z_1+z_2=(\;x_1+x_2,\;y_1+y_2\;)\);
- \(z_1\cdot z_2=(\;x_1x_2-y_1y_2,\;x_1y_2+x_2y_1\;)\).
Niech \(z_1\), \(z_2\), \(z_3\) będą dowolnymi liczbami zespolonymi. Wtedy
- \(z_1+z_2=z_2+z_1\;\) (przemienność dodawania);
- \((z_1+z_2)+z_3=z_1+(z_2+z_3)\;\) (łączność dodawania);
- \(z_1+{\bf 0}=z_1\;\), gdzie \({\bf 0}=(0,0)\;\) (element neutralny dodawania);
- \(z_1+(-z_1)={\bf 0}\;\) (element przeciwny względem dodawania);
- \(z_1\cdot z_2=z_2\cdot z_1\;\) (przemienność mnożenia);
- \((z_1\cdot z_2)\cdot z_3=z_1\cdot (z_2\cdot z_3)\;\) (łączność mnożenia);
- \(z_1\cdot {\bf 1}=z_1\;\), gdzie \({\bf 1}=(1,0)\;\) (element neutralny mnożenia);
- \(z_1\cdot \displaystyle\frac{1}{z_1}={\bf 1}\;\) dla \(z_1\neq 0\) (element odwrotny względem mnożenia);
- \(z_1\cdot (z_2+z_3)=z_1\cdot z_2+z_1\cdot z_3\;\) (rozdzielność mnożenia względem dodawania).
Zapamiętaj - to jest ważne
Zbiór liczb rzeczywistych jest podzbiorem zbioru liczb zespolonych, tzn. można utożsamić zbiór liczb rzeczywistych \(\mathbb{R}\) ze zbiorem
\(\color{red}{\mathbb{R}^*=\{(x,0)\;:\;\;\;x\in \mathbb{R}\}}\;\).
Definicja
Jednostką urojoną (oznaczaną przez \(i\)) nazywamy liczbę zespoloną postaci
\(\;\color{red}{i=(0,1)}\;\).