Postać algebraiczna liczby zespolonej
Postać algebraiczna liczby zespolonej
Każdą liczbę zespoloną można jednoznacznie zapisać w postaci
\(\color{red}{z=x+iy}\)
gdzie \(x,y\in \mathbb{R}\). Postać tę nazywamy postacią algebraiczną liczby zespolonej.
Definicja
Niech \(x+iy\) będzie postacią algebraiczną dowolnej liczby zespolonej \(z\). Wówczas
- liczbę \(x\) nazywamy częścią rzeczywistą liczby zespolonej i oznaczamy \(\textcolor{red}{Re\;z=x}\;\);
- liczbę \(y\) nazywamy częścią urojoną liczby zespolonej i oznaczamy \(\textcolor{red}{Im\;z=y}\;\).
Liczbę postaci \(iy\) nazywamy czysto urojoną.
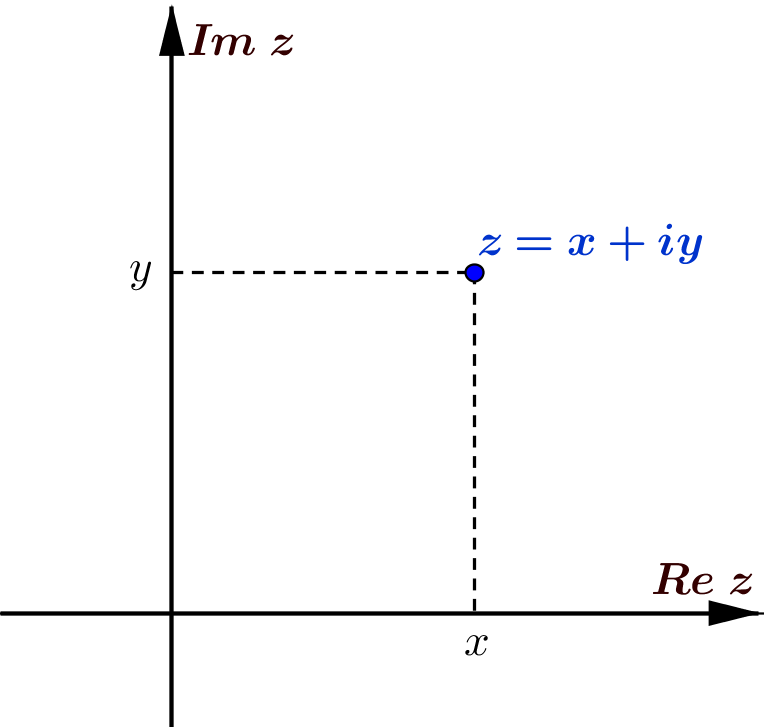
Zapamiętaj - to jest ważne
Działania na liczbach zespolonych w postaci algebraicznej wykonujemy tak jak na wielomianach zmiennej \(i\), przy warunku
\(\textcolor{red}{i^2=-1}\;\).
Z postacią algebraiczną liczby zespolonej związane są takie pojęcia jak:
- sprzężenie liczby zespolonej
- moduł liczby zespolonej
- argument liczby zespolonej
Zostaną one poniżej kolejno omówione.
SPRZĘŻENIE LICZBY ZESPOLONEJ
Definicja
Sprzężeniem liczby zespolonej \(z=x+iy\), gdzie \(x,y\in \mathbb{R}\), nazywamy liczbę zespoloną \(\bar{z}\) określoną wzorem
\(\textcolor{red}{\bar{z}=x-iy}\;\).
Własności sprzężenia liczby zespolonej
- \(\overline{{z_1+z_2}}=\overline{z_1}+\overline{z_2}\;\);
- \(\overline{{z_1-z_2}}=\overline{z_1}-\overline{z_2}\;\);
- \(\overline{z_1\cdot z_2}=\overline{z_1}\cdot \overline{z_2}\;\);
- \(\overline{\;\bigg(\;\displaystyle\frac{z_1}{z_2}\;\bigg)\;}=\displaystyle\frac{\overline{z_1}}{\overline{z_2}}\;\);
- \(\overline{(\bar{z})}=z\;\)
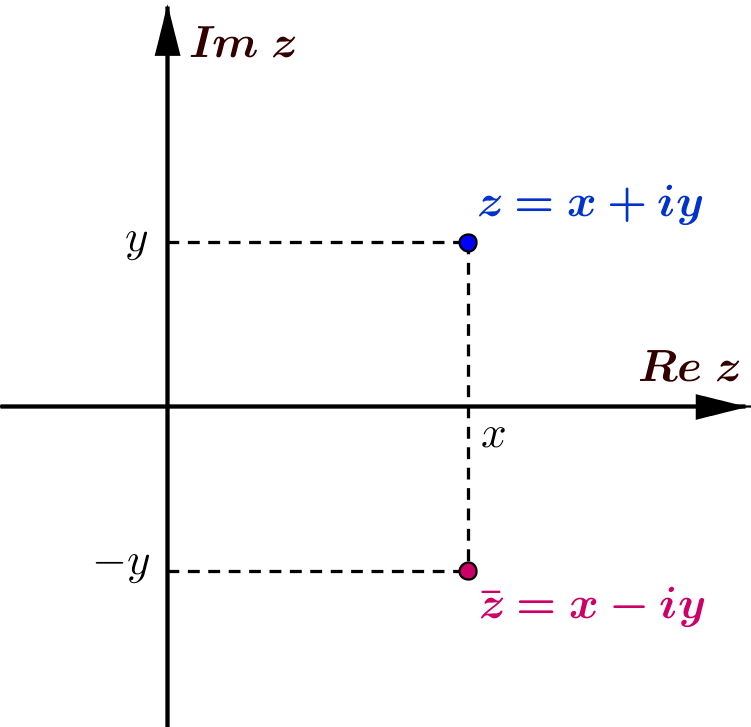
MODUŁ LICZBY ZESPOLONEJ
Definicja
Modułem liczby zespolonej \(z=x+iy\), gdzie \(x,y\in \mathbb{R}\), nazywamy liczbę rzeczywistą \(|z|\) określoną wzorem
\(\textcolor{red}{|z|=\sqrt{x^2+y^2}}\;\).
Własności modułu liczby zespolonej
- \(|\bar{z}|=|z|=|-z|\);
- \(\;z\cdot \bar{z}=|z|^2\);
- \(|z_1\cdot z_2|=|z_1|\cdot |z_2|\;\);
- \(\bigg|\;\displaystyle\frac{z_1}{z_2}\;\bigg|=\displaystyle\frac{|z_1|}{|z_2|}\);
- \(|z_1+z_2|\leqslant |z_1|+|z_2|\).
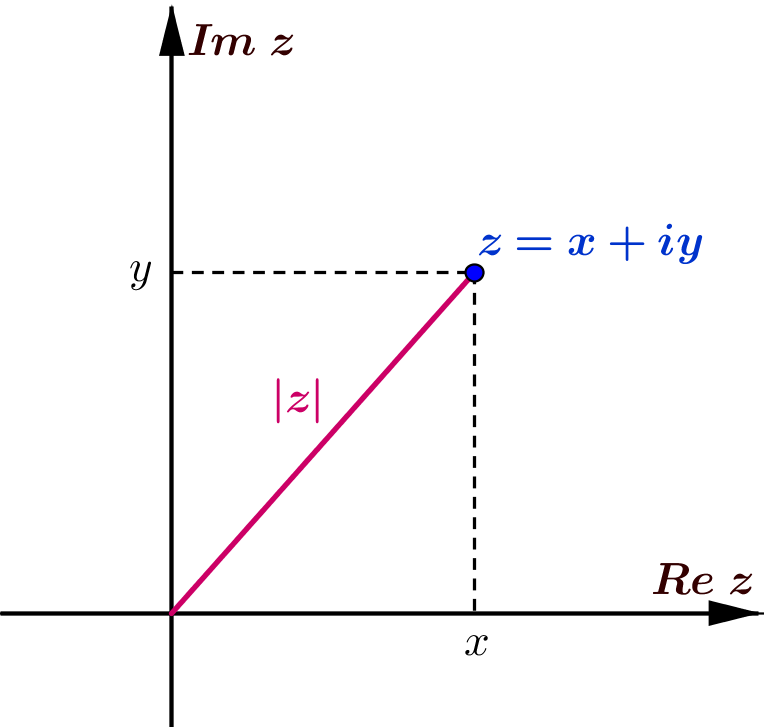
ARGUMENT LICZBY ZESPOLONEJ
Definicja
Argumentem liczby zespolonej \(z=x+iy\neq 0\), gdzie \(x,y\in \mathbb{R}\), nazywamy każdą liczbę rzeczywistą \(\varphi \) spełniającą układ równań
\(\left\{\textcolor{red}{
\begin{array}{c}
\;\cos \varphi =\dfrac{x}{|z|}\;\\(3ex]
\;\sin \varphi =\dfrac{y}{|z|}\;\\
\end{array}}\right..\)
Przyjmiemy, że argumentem liczby zespolonej \(z=0\) jest każda liczba \(\varphi \in \mathbb{R}\).

Argumentem głównym liczby zespolonej \(z\) (oznaczamy \(arg\;z\)) nazywamy argument \(\varphi \) tej liczby spełniający nierówności
\(\textcolor{red}{0\leq \varphi <2\pi }\;\).
Przyjmujemy, że argumentem głównym liczby \(z=0\) jest \(0\).
Czasami wygodnie jest przyjąć, że argument główny liczby zespolonej jest liczbą z przedziału \(\textcolor{red}{(-\pi, \pi>}\).
Własności argumentu liczby zespolonej
- \(arg\;(\bar{z})=2\pi - arg\;z\;\);
- \(arg\;\biggl(\;\dfrac{1}{z}\;\biggr)=2\pi - arg\;z\);
- \(arg\;(z^n)=n\cdot arg\;z+2k\pi\);
- \(arg\; \dfrac { z _ { 1 } } { z _ { 2 } } = arg\;z _ { 1 } - arg \;z _ { 2 } + 2 k \pi\)