Postać trygonometryczna liczby zespolonej
Postać trygonometryczna liczby zespolonej
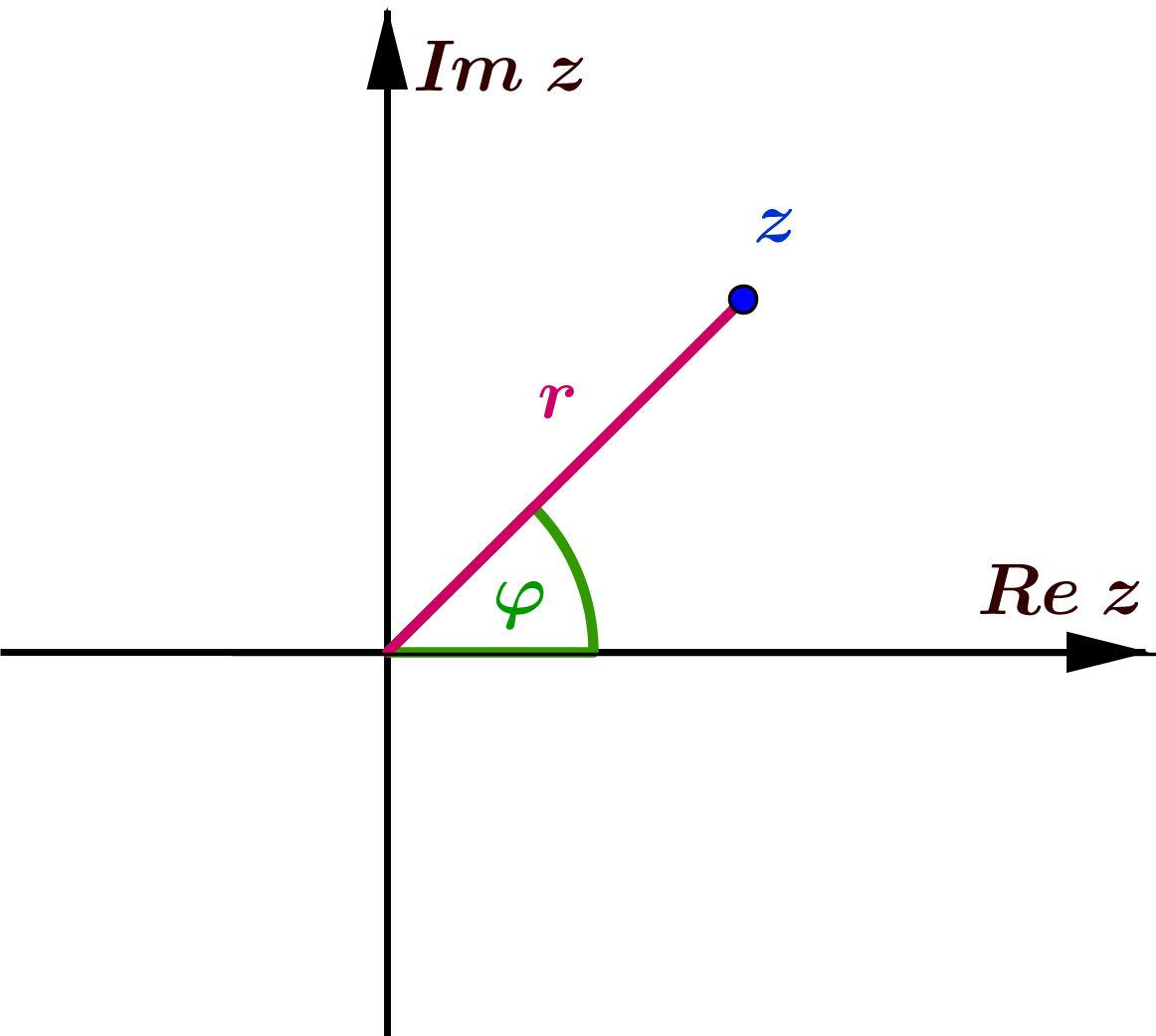
Każdą liczbę zespoloną można przedstawić w postaci
\(\textcolor{red}{z=r(\cos \varphi +i\sin \varphi )}\;\),
gdzie \(r\geqslant 0\) oraz \(\varphi \in \mathbb{R}\). Liczba \(r\) jest wówczas modułem liczby \(z\), a \(\varphi \) jednym z jej argumentów.
Liczby zespolone \(z_1=r_1(\cos \varphi _1 +i\sin \varphi _1)\) oraz \(z_2=r_2(\cos \varphi _2 +i\sin \varphi _2)\), gdzie \(r_1\), \(r_2\geqslant 0\) oraz \(\varphi _1\), \(\varphi _2 \in \mathbb{R}\), są równe wtedy i tylko wtedy, gdy
\(r_1=r_2\)
oraz
\(\varphi _1=\varphi _2+2k\pi \)
dla pewnego \(k\in \mathbb{Z}\).
Mnożenie i dzielenie liczb zespolonych w postaci trygonometrycznej
Niech \(z_1=r_1(\cos \varphi _1 +i\sin \varphi _1)\) oraz \(z_2=r_2(\cos \varphi _2 +i\sin \varphi _2)\), gdzie \(r_1, r_2 > 0\) oraz \(\varphi _1\), \(\varphi _2 \in \mathbb{R}\). Wówczas
- \(z _ { 1 } \cdot z _ { 2 } = r _ { 1 } \cdot r _ { 2 } \begin{bmatrix} { \cos \left( \varphi _1 + \varphi _2 \right) + i \sin \left( \varphi _1 + \varphi _2 \right) } \end{bmatrix}\)
- \(\dfrac { z _ { 1 } } { z _ { 2 } }=\dfrac { r _ { 1 } } { r _ { 2 } } \begin{bmatrix} { \cos \left( \varphi _1 - \varphi _2 \right) + i \sin \left( \varphi _1 - \varphi _2 \right) } \end{bmatrix}\)
Działania na liczbach zespolonych w postaci trygonometrycznej
Niech \(z=r(\cos \varphi +i\;\sin \varphi )\), gdzie \(r>0\) oraz \(\varphi \in \mathbb{R}\;\). Wówczas
- \(\;\bar{z}=r\;[\;\cos (-\varphi )+i\;\sin (-\varphi )\;]\;\),
- \(\;-z=r\;[\;\cos (\varphi +\pi)+i\;\sin (\varphi +\pi)\;]\;\),
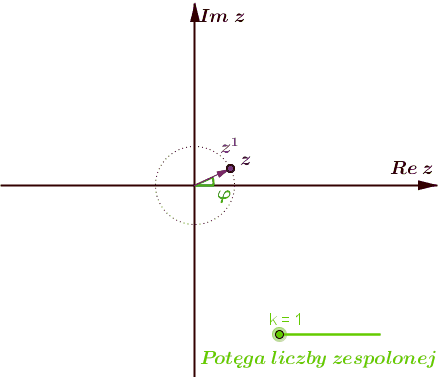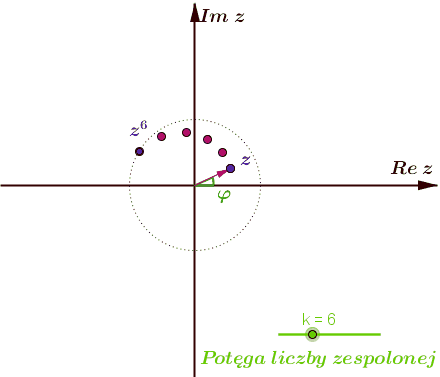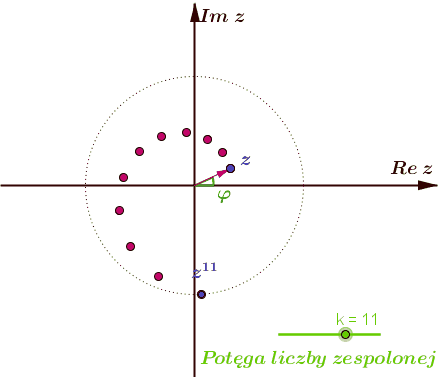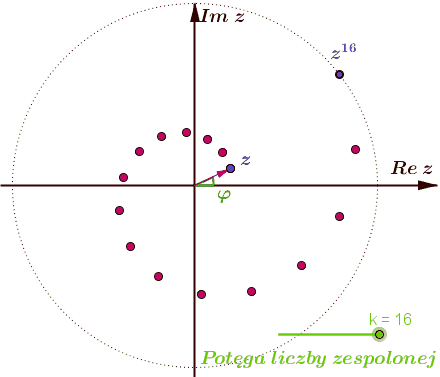
- \(\;\textcolor{red}{z^k=r^k\;[\;\cos (k\varphi )+i\;\sin (k\varphi )\;]}\;\).
Dla \(k \in \mathbb{N}\;\) trzecia równość nosi nazwę wzoru de Moivre'a.
PIERWIASTKOWANIE LICZB ZESPOLONYCH
Definicja
Pierwiastkiem stopnia\(n\in \mathbb{N}\) z liczby zespolonej \(z\) nazywamy każdą liczbę zespoloną \(w\) spełniającą równość \(\textcolor{red}{w^n=z}\;\).
Zbiór pierwiastków stopnia \(n\) z liczby zespolonej \(z\) oznaczamy przez \(\root n\of{z}\).
Zapamiętaj - to jest ważne
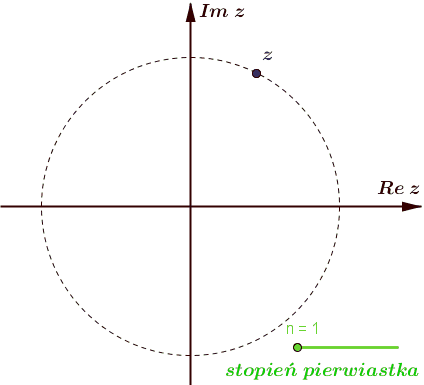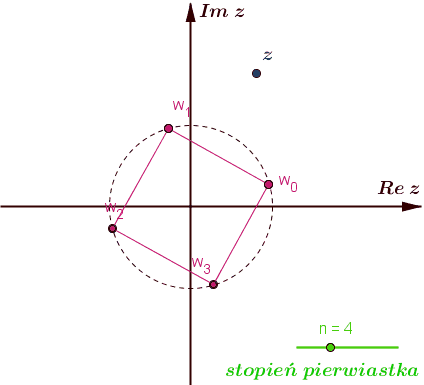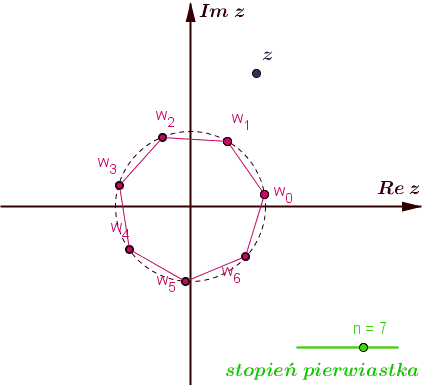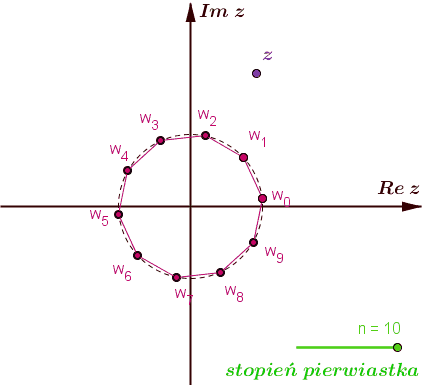
Zbiór pierwiastków stopnia \(n\geqslant 3\) z liczby zespolonej \(z=r(\cos \varphi +i\sin \varphi )\) pokrywa się ze zbiorem wierzchołków \(n\) -kąta foremnego wpisanego w okrąg o promieniu \(\root n\of{r}\) i środku w początku układu współrzędnych.
Zapamiętaj - to jest ważne
Wzór na pierwiastki z liczby zespolonej
Każda liczba zespolona \(z=r(\cos \varphi +i\sin \varphi )\), gdzie \(r>0\) oraz \(\varphi \in \mathbb{R}\), ma dokładnie \(n\) pierwiastków stopnia \(n\):
\(\textcolor{red}{\root n\of{z}=\{z_0,z_1,\ldots ,z_{n-1}\}}\;\),
gdzie
\(\textcolor{red}{z_k=\root n\of{r}\;\biggl(\;\cos \displaystyle\frac{\varphi +2k\pi}{n}+i\;\sin \displaystyle\frac{\varphi +2k\pi}{n}\;\biggr)}\)
dla \(k=0,1,\ldots ,n-1\).