Postać wykładnicza liczby zespolonej (dla zainteresowanych)

Wzory Eulera

Niech \(\varphi \in \mathbb{R}\). Wówczas zachodzą wzory

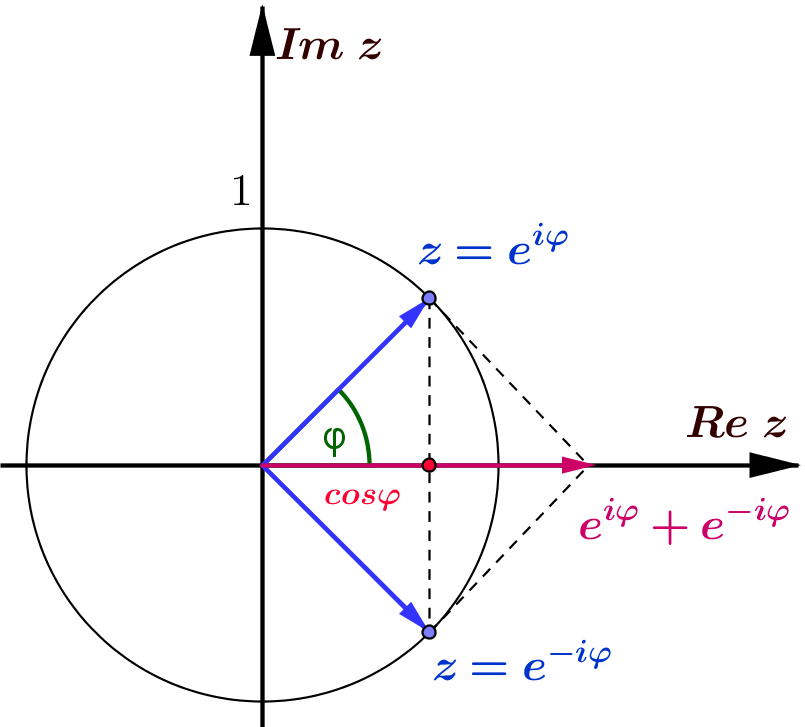
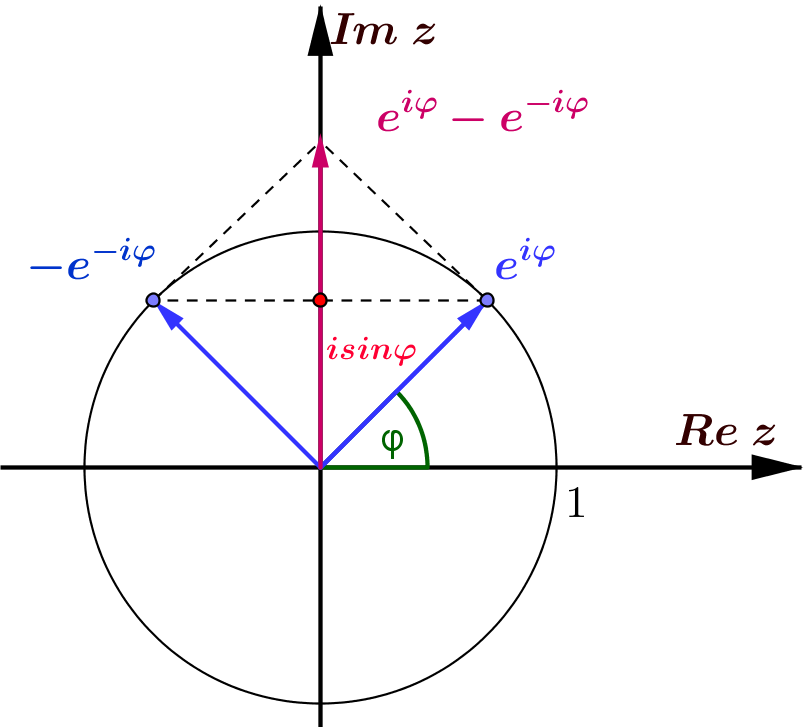
\(\textcolor{red}{\cos \varphi =\displaystyle\frac{e^{\;i\varphi}+e^{\;-i\varphi}}{2}}\;,\quad \textcolor{red}{\sin \varphi =\displaystyle\frac{e^{\;i\varphi}-e^{\;-i\varphi}}{2i}\;}\)

     
Własności

• \(e^{\;i\varphi}\ne 0\;\);
• \(|\;e^{\;i\varphi}\;|=1\;\)

Postać wykładnicza liczby zespolonej

Każdą liczbę zespoloną \(z\) można zapisać w postaci wykładniczej

\(\textcolor{red}{z=r\;e^{\;i\varphi}}\;,\)

gdzie \(r>0\) oraz \(\varphi \in \mathbb{R}\).  Liczba \(r\) jest wówczas modułem liczby \(z\), a \(\varphi \) jej argumentem.

Liczby zespolone \(z_1=r_1e^{\;i\varphi_1}\) oraz \(z_2=r_2e^{\;i\varphi_2}\), gdzie \(r_1\), \(r_2\geqslant 0\) oraz \(\varphi _1\), \(\varphi _2 \in \mathbb{R}\), są równe wtedy i tylko wtedy, gdy

\(r_1=r_2\)

oraz

\(\varphi _1=\varphi _2+2k\pi \)

dla pewnego \(k\in \mathbb{Z}\).

Mnożenie i dzielenie liczb zespolonych w postaci wykładniczej

Niech \(z_1=r_1e^{\;i\varphi_1}\)  oraz  \(z_2=r_2e^{\;i\varphi_2}\),  gdzie \(r_1, r_2 > 0\)  oraz  \(\varphi _1\), \(\varphi _2 \in \mathbb{R}\). Wówczas

• \(z _ { 1 } \cdot z _ { 2 } = r _ { 1 } r _ { 2 }e^{\;i(\varphi_1+\varphi_2)}\)
  

• \(\dfrac { z _ { 1 } } { z _ { 2 } }=\dfrac { r _ { 1 } } { r _ { 2 } }e^{\;i(\varphi_1-\varphi_2)}\),  o ile \(z _ { 2 } \neq 0\)

Działania na liczbach zespolonych w postaci wykładniczej

• \(\bar{z}=re^{\;-i\varphi}\;\);
• \(-z=re^{\;i(\varphi +\pi)}\;\);
• \(z^k=r^ke^{\;ik\varphi}\;\);
• Niech \(z\neq 0\) i niech \(z=re^{i\varphi}\). Wtedy

\(z_k=\root n \of{r}\;\;e^{i\;\frac{\varphi}{n}}\;e^{i\;\frac{2k\pi}{n}}=z_0\bigg(e^{i\;\frac{2\pi}{n}}\bigg)^k\) dla \(k=1, 2, \ldots , n-1\).

Pierwiastki \(n\)-tego stopnia z liczby \(z\) tworzą wierzchołki \(n\)-kąta foremnego wpisanego w okrąg o środku w początku układu współrzędnych i promieniu \(\root n \of{r}\).