Szacujemy pochodną z wykresu

Na wykresie funkcji zostało wyróżnione pięć punktów. Uporządkujmy pochodne w tych punktach, od najmniejszej do największej.

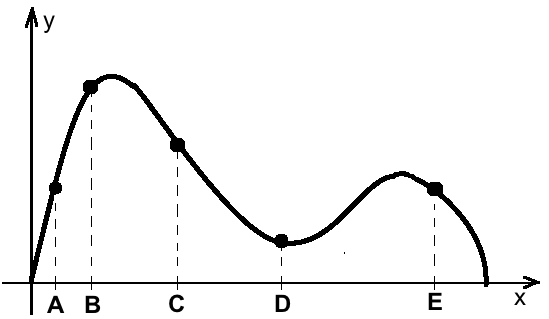
Tutaj nie musimy liczyć przybliżonych wartości pochodnych, wystarczy określić w których punktach funkcja rośnie lub maleje, szybciej lub wolniej.

I tak:

• funkcja rośnie w   \(x=A\)  i  \(x=B\)
• funkcja maleje w  \(x=C,D,E\)

Naszkicowanie stycznych w tych punktach ułatwi nam określenie jak szybko funkcja zmienia się w porównaniu do innych punktów.

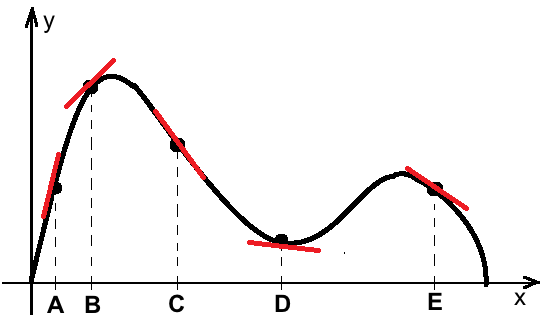
Widać z tego wyraźnie, że:

• w punkcie  \(x=A\)  funkcja rośnie szybciej niż w  \(x=B\)
• w \(C\) funkcja maleje nieznacznie szybciej niż w  \(E\),  więc pochodna będzie bardziej ujemna w  \(C\)
• w punkcie  \(D\)  styczna jest prawie pozioma, prędkość przyrostu jest zatem ujemna, ale bliska zeru.

Mamy zatem następującą kolejność:

\(f'(C)<f'(E)<f'(D)<f'(B)<f'(A)\)