Co to są przyrosty powiązane i jak sobie z nimi radzić

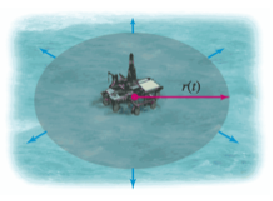
Dwie wielkości zmieniają się tutaj jednocześnie: promień i pole koła. Związek między tymi dwiema wielkościami zawarty jest oczywiście we wzorze na pole:  \(A=\pi r^2\). 

Aby podkreślić, że zarówno promień  \(r\)  jak i pole  \(A\)  zmieniają się w czasie, wygodnie jest użyć oznaczeń  \(r(t)\)  i  \(A(t)\).  Wówczas wzór na pole, dający związek między polem i promieniem w każdym momencie czasu, zapisujemy

\(A(t) = \pi r(t)^2\)

Celem jest znalezienie prędkości z jaką zwiększa się pole koła, a prędkość wzrostu funkcji to pochodna funkcji,  \(A'(t)\), natomiast prędkość z jaką zmienia się promień  \(r'(t)\)  znamy z treści zadania.  Podsumujmy co wiemy a czego szukamy:

Pole i promień cały czas rosną, ale zasadnicza różnica jest taka, że promień zwiększa się ze stałą prędkością 30m/h, pole natomiast rośnie coraz szybciej (przyjrzyj się animacji obok). My szukamy prędkości z jaką rośnie pole w momencie gdy promień wynosi dokładnie 100m.

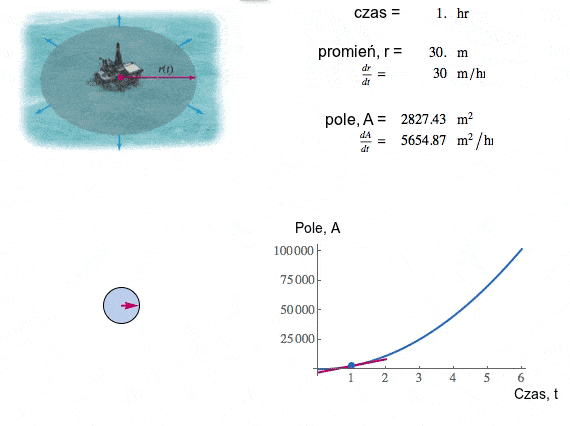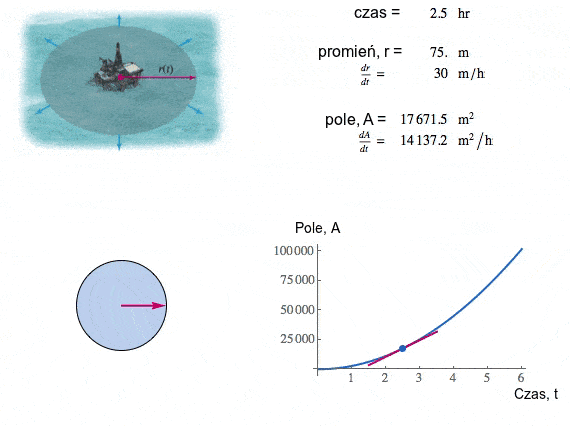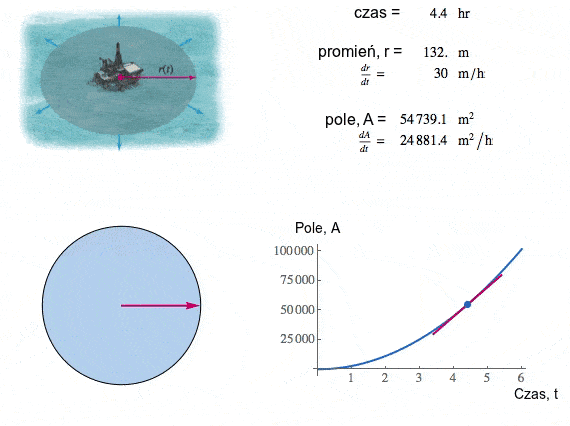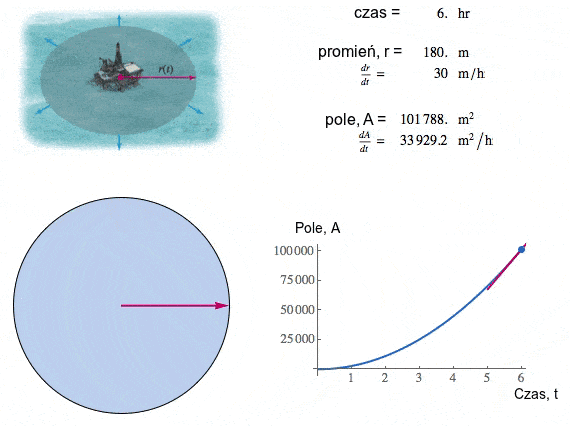
Calculus, Briggs Cochran

Skoro musimy znaleźć wartość  \(A'(t)\) , to musimy policzyć pochodną naszego równania

\(A(t) =\pi r(t)^2\)

\(\frac{d}{dt}\left[A(t)\right]=\frac{d}{dt}\left[\pi r(t)^2\right]\)

\(\frac{dA}{dt} = \pi\frac{d}{dt}\left[r(t)^2\right]\)

teraz musimy skorzystać ze wzoru na pochodną funkcji złożonej, czyli

\(\frac{dA}{dt} = \pi\cdot \frac{d\left[(r(t))^2\right]}{d(r(t))}\cdot \frac{d(r(t))}{dt}\)

\(\frac{dA}{dt} = \pi\cdot 2r(t)\cdot \frac{d(r(t))}{dt}\)

\(A'(t)=2\pi r(t)\cdot r'(t)\)

Teraz pozostaje tylko podstawić dane wartości:

\(A'(t)=2\pi\left(100m\right)\left(30\frac{m}{h}\right)\)

i uprościć

\(A'(t)=6000\pi \frac{m^2}{h}\)

Czyli pole powierzchni plamy ropy zwiększa się z prędkością  \(6000\pi\approx 18850 m^2/h\), w momencie gdy promień wynosi 100m. Włączenie jednostek do obliczeń to łatwy sposób na sprawdzenie czy wzory zostały zapisane poprawnie. W tym zadaniu spodziewamy się otrzymać odpowiedź w jednostkach pola powierzchni przez czas, więc  \(m^2/h\)  ma sens.