Jak znaleźć ekstrema funkcji ?
Jak znaleźć ekstrema funkcji ?
Deja vu
O związku znaku pochodnej z monotonicznością funkcji już było
Związek między monotonicznością funkcji a znakiem jej pochodnej
Gdy funkcja rośnie -- przyrost wartości jest dodatni, pochodna jest dodatnia.
Gdy funkcja maleje -- przyrost wartości jest ujemny, pochodna jest ujemna.
Gdy funkcja jest stała -- przyrost wartości jest zerowy, pochodna równa się zero.
A kiedy funkcja osiąga wartości największe i najmniejsze, tzw. ekstrema lokalne ?
|
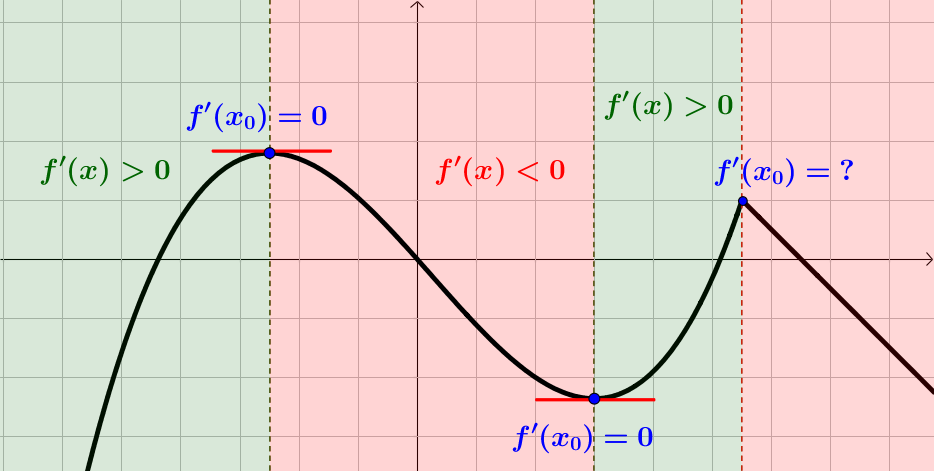
Przyjżyj się przykładowemu wykresowi po prawej. W punktach, w których funkcja osiąga ekstremalne wartości, pochodna jest równa zero albo nie da się jej policzyć. W pozostałych punktach pochodna jest dodatnia lub ujemna. |
 |
 |
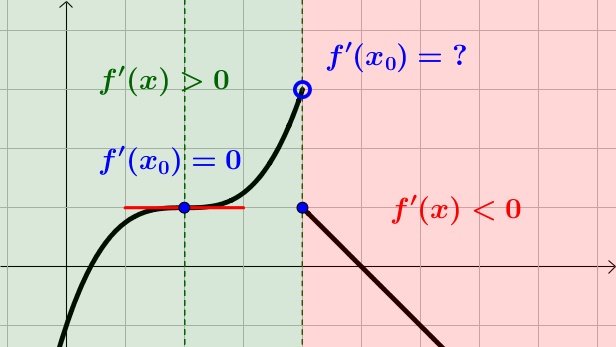Ale, jak widać na wykresie po lewej f'(x)=0 lub f'(x)=? nie gwarantuje istnienia ekstremum Jeżeli pochodna nie zmienia znaku, to funkcja nie zmienia monotoniczności. Jeżeli przedział jest otwarty \([a,b)\) to w punkcie x=b może nie być osiągnięta najmniejsza lub największa wartość. |
Kiedy funkcja posiada ekstremum - wartość największą bądź najmniejszą - w punkcie \(x_0\) ?
Warunek konieczny
Funkcja może posiadać ekstremum tylko w punktach, w których
\(f'(x_0)=0\) lub \(f'(x_0)\) nie istnieje
Są to tzw. punkty krytyczne.
Warunek dostateczny
Aby punkt krytyczny był ekstremum, funkcja musi zmieniać monotoniczność wokół tego punktu, czyli
\(f'(x)\) musi zmieniać znak wokół punktu \(x_0\)
- Jeżeli \(f'(x)\) zmienia znak z \(+\) na \(-\) to punkt \(x_0\) jest maksimum lokalnym
- Jeżeli \(f'(x)\) zmienia znak z \(-\) na \(+\) to punkt \(x_0\) jest minimum lokalnym
