Zadanie: 3-metrowy płot jest postawiony równolegle do budynku w odległości 2 metrów od niego. Budynek ma wysokość 15 m. Jaka jest długość najkrótszej drabiny, którą można oprzeć o ścianę domu tak aby nie "wisiała" na płocie ?
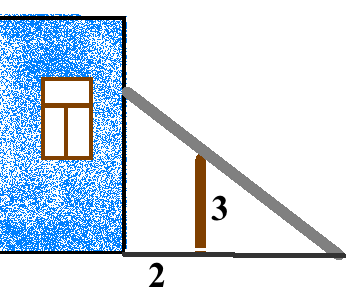
Rozwiązanie:
Identyfikujemy zmienne i funkcję:
Zacznijmy od szkicu sytuacji i naniesienia stałych i zmiennych.
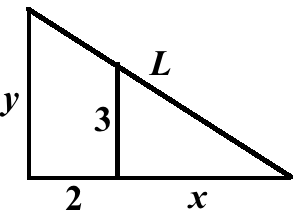
Chcemy znaleźć najmniejszą długość drabiny, zatem potrzebne jest nam równanie na \(L\). Twierdzenie Pitagorasa będzie tu idealne:
\((2+x)^2+y^2=L^2\)
Jedną z liter należy stąd wyeliminować. Możemy się do tego posłużyć trójkątami podobnymi, bo
\(\frac{x}{3}=\frac{x+2}{y}\quad\Longrightarrow\quad y=\frac{3(x+2)}{x}\)
Wykorzystując to, możemy zapisać nasze równanie jako funkcję jednej zmiennej,
\(L^2=(x+2)^2+\frac{9}{x^2}(x+2)^2\)
Jawny wzór na \(L\)to
\(L(x)=\sqrt{(x+2)^2+\frac{9}{x^2}(x+2)^2}\)
Liczymy:
Liczymy pochodną naszej funkcji (używając Geogebry)
\(L'(x)=\frac{x^4+2x^3-18x-36}{x^3\sqrt{(x+2)^2+9\cdot\frac{(x+2)^2}{x^2}}}\)
i szukamy punktów krytycznych (również przy pomocy Geogebry)
\(L'(x)=0\quad\Leftrightarrow\quad x=\sqrt[3]{18}\approx 2.62\)
Pochodna nie istnieje dla \(x=0\), ale nie ma to praktycznego sensu, więc ten punkt pomijamy.
Z wykresu pochodnej widać, że jest to szukane minimum (widać to też z wykresu funkcji \(L(x)\)).
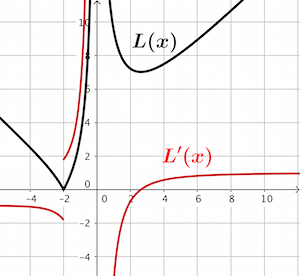
Zatem najkrótsza drabina spełniająca warunki zadania ma długość
\(L(\sqrt[3]{18})\approx 7 m\)


