Zadanie: Regulamin pewnej linii lotniczej mówi, że bagaż musi być w kształcie prostopadłościaniu i że suma jego wysokości, długości i szerokości nie może przekraczać 160 cm. Jakie wymiary bagażu o podstawie kwadratu maksymalizują jego objętość ?
Rozwiązanie:
Identyfikujemy zmienne i funkcję:
Prostopadłościan ma mieć podstawę kwadratu, więc oznaczmy przez \(w\) długość podstawy i przez \(h\) jego wysokość.
Suma długości, szerokości i wysokości ma mieć nie więcej jak 160 cm, więc wykorzystajmy to w całości, czyli
\(2w+h=160\)
Mamy znaleźć maksymalną objętość
\(V=w^2\cdot h\)
Wykorzystując zadane ograniczenie, możemy zapisać objętość jako funkcję jednej zmiennej, czyli
\(h=160-2w\)
\(V(w)=w^2\cdot(160-2w)=160w^2-2w^3\)
Liczymy:
|
Liczymy pochodną naszej funkcji
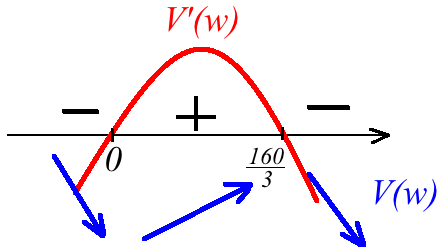
\(V'(w)=320w-6w^2\)
i szukamy punktów krytycznych
\(V'(w)=0\quad\Leftrightarrow\quad w(320-6w)=0\)
zatem \(w=0\quad\vee\quad w=\frac{160}{3}\)
|
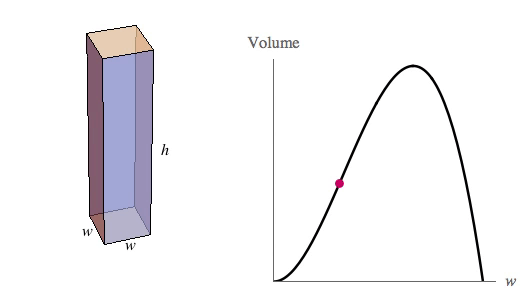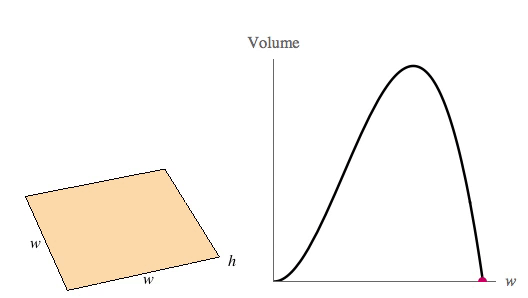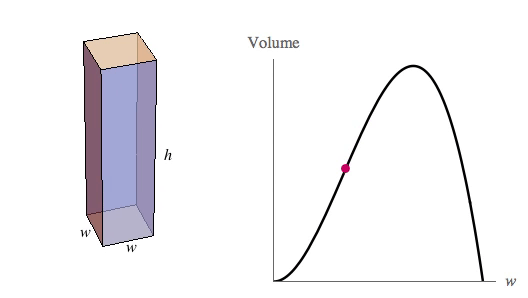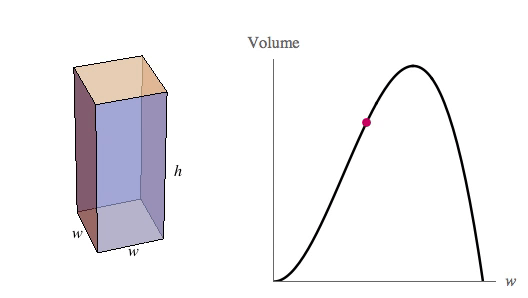 |
Funkcja ma jedno maksimum i jedno miminum. Nas interesuje oczywiście maksimum, czyli \(w=\frac{160}{3}\).
Zatem wymiary bagażu, które maksymalizują jego objętość to
\(\frac{160}{3}cm\times\frac{160}{3}cm\times\frac{160}{3}\)
Okazuje się, że jest to sześcian.

