Modele epidemiologiczne
Modele epidemiologiczne
Model SIS
W modelu SI oczywiście nie było szans na to aby ocalić społeczeństwo - no i są takie choroby z których wyjść się nie da. Model SI możemy zmodyfikować przez dodanie możliwości wyzdrowienia przez osobę zainfekowaną.
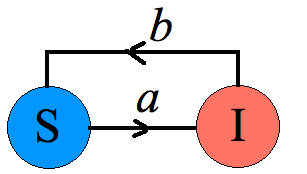
Czyli tutaj obie grupy zmieniają się dodatkowo przez to, że częśś osobników z grupy zainfekowanej wyzdrowieje i wróci do grupy podatnej na chorobę. Czyli \(S\) się powiększy, a \(I\) zmniejszy się o tę samą wielkość. Zatem
\(\begin{cases}S'(t)=-aSI+bI\\ I'(t)=aSI-bI\end{cases}\)
W poniższym aplecie wpisz następujące zastawy parametrów i przyjżyj się wynikom. Czy dla jakichś wartości epidemia teraz jest do opanowania ?
\(\begin{cases}a=0.0004\\ b=0.1\\S(0)=950\\ I(0)=50\end{cases}\quad \begin{cases}a=0.0002\\ b=0.1\\S(0)=950\\ I(0)=50\end{cases}\quad \begin{cases} a=0.001\\ b=0.1\\S(0)=950\\ I(0)=50\end{cases}\quad \begin{cases}a=0.0001\\b=0.1\\ S(0)=400\\ I(0)=600\end{cases}\)
![]() Co się dzieje
Co się dzieje
Zredukujmy ten układ do jednego równania dla \(I'(t)\) , znowu korzystając z tego, że \(N=S+I\)
\(I'(t)=(aS-b)I=a\left(S-\frac{b}{a}\right)I\)
\(I'(t)=a\left(N-\frac{b}{a}-I\right)I\)
I znowu mamy model logistyczny, a ten już wiemy jak przeanalizować.
- Są dwa rozwiązania stałe: \(I=0\) oraz \(I=N-\frac{b}{a}\)
- \(N\) jest stałe i w zależności od tego czy \(N-\frac{b}{a}\) jest większe, mniejsze, czy równe zero, będziemy mieli różne zachowania
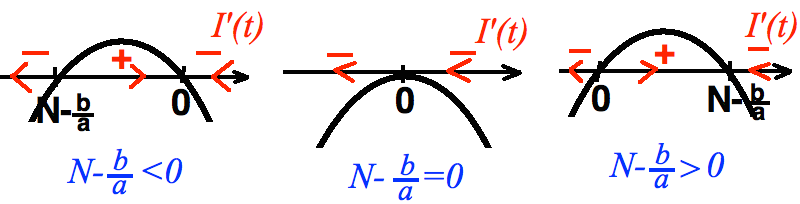
Czyli jeżeli \(N\leq\frac{b}{a}\) , to \(I(t)\) będzie malała do zera !
Narysuj sobie rozwiązania jeszcze raz i teraz zwróć uwagę na to czy \(N=1000\) jest większe czy mniejsze (bądź równe) od \(\frac{b}{a}\) .