Modele epidemiologiczne

Model Kermacka-McKendricka, potocznie zwany modelem SIR, jest jeszcze bardziej rozbudowany niż poprzednie dwa. W tym modelu występuje trzecia grupa osobników - wyleczonych (lub odpornych na infekcje) ozn.   \(R\) .

Schemat zachowania modelu wygląda tak

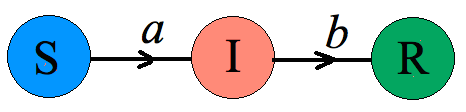
Czyli podobnie jak poprzednio, osobnik podatny może zachorować, więc S maleje, a I rośnie z tą samą prędkością. Dodatkowo osobnik zainfekowany może wyzdrowieć i "przenieść się" do grupy R, jednocześnie ta nowa grupa będzie rosła. Czyli

\(\begin{cases}S'(t)=-aSI\\I'(t)=aSI-bI\\ R'(t)=bI\end{cases}\)

Tym razem chyba nie ma potrzeby przeprowadzania analizy jakościowej, bo tak na logikę biorąc, skoro wszystkie strzałki są w jedną stronę, to w końcu wszyscy wyzdrowieją. Kwestia tylko jak długo to będzie trwało i jak dokładnie będzie się układało w czasie