Modele epidemiologiczne
Modele epidemiologiczne
Inne wariacje
Teraz znasz już podstawowe zasady z których można budować modele epidemiologiczne. Model SIR jest podstawowym i możesz go rozszerzać przez dodawanie innych elementów.
Istotnym elementem walki z chorobami zakaźnymi są szczepienia. Możemy do naszego modelu SIR dodać jeszcze jedną grupę, V(t), czyli zaszczepionych. Jak ją połączyć z istniejącym modelem ? Pewnie szczepić trzeba dzieci i dorosłych zanim zachorują, więc może tak
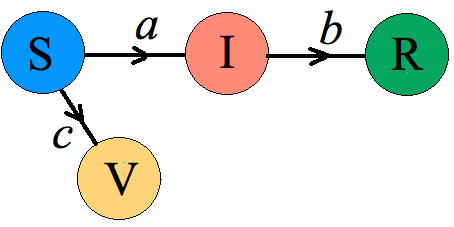
Jak wyglądają równania opisujące tą dynamikę ?
\(\begin{cases}S'(t)=-aSI-cS\\I'(t)=aSI-bI\\ R'(t)=bI\\V'(t)=cS\end{cases}\)
A gdyby tak choroba, którą chcemy "zamodelować" ma taką własność, że osobnik, który przeszedł chorobę i wyzdrowiał, nie staje się na nią odporny, ale jest (może po jakimś czasie) znowu podatny. Czyli coś takiego
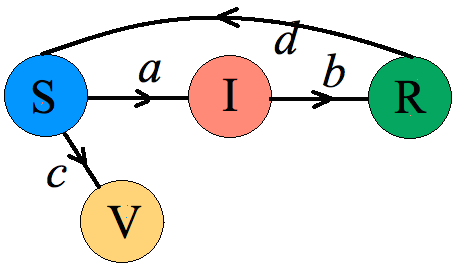
Jak teraz będą wyglądały równania ?
\(\begin{cases}S'(t)=-aSI-cS+dR\\I'(t)=aSI-bI\\ R'(t)=bI-dR\\V'(t)=cS\end{cases}\)
Jak widzisz w sumie wszystko opiera się na składnikach typu "Malthusa" i typu "logistycznego". Z tych klocków możesz teraz budować bardziej skomplikowane modele.
Można też dodwać opóźnienie czasowe, wówczas np. zamiast \(dR(t)\) można wstawić składnik \(dR(t-t_0)\) , aby to przejście z ostatniego przykładu osobnika wyzdrowiałego do grupy podatnych, następowało z opóźnieniem czasowym \(t_0\) .
I tak dalej, i tak dalej...