Macierze i układy równań
Macierze i układy równań
Wyznaczniki, odwrotności, rzędy i rozwiązywanie równań metodą macierzy odwrotnej.
Zadanie (9)
Stwórz macierz kwadratową o dowolnych (ale sensownych – czyli nie np. 119x119) wymiarach i wypełnij ją dowolnymi liczbami. Wypróbuj następujące komendy:
>> det(A) % wyznacznik macierzy
>> rank(A) % rząd macierzy
>> trace(A) % ślad macierzy
>> null(A) % jądro macierzy
>> eig(A) % wektory wartości własne macierzy
>> inv(A) % macierz odwrotna
>> poly(A) % współczynniki wielomianu charakterystycznego macierzy
>> svd(A) % rozkład według wartości osobliwych macierzy
>> R=chol(A) % faktoryzacja Choleskiego, czyli A = R'*R
>> [L U] = lu(A) % faktoryzacja LU, czyli A = L*U
>> [Q R] = qr(A) % faktoryzacja QR, czyli A = Q*R
Sprawdź, jak działają powyższe polecenia, gdy A nie jest macierzą kwadratową.
Podstawową metodą rozwiązywania układów liniowych jest metoda eliminacji Gaussa – tzw. rozkład LU. Polega on na znalezieniu macierzy L i U takich, że A=L*U, gdzie U jest macierzą trójkątną górną, a L macierzą trójkątną dolną. W MATLABie eliminację Gaussa przeprowadza funkcja lu. Przy wywołaniu [L,U]=lu(A) U jest macierzą trójkątną górną, ale L nie zawsze będzie macierzą trójkątną dolną! Przy wywołaniu [L,U,P]=lu(A) U jest macierzą trójkątną górną, L nie zawsze będzie macierzą trójkątną dolną, a P jest macierzą permutacji (zmienia kolejność wierszy w macierzy A). Zachodzi tu zależność L*U=P*A.
Zadanie (10)
Utwórz odpowiednie macierze dla przykładu:
![]()
zn. do macierzy A wpisz wartości macierzy danej po lewej stronie, do macierzy B wpisz wartości macierzy danej po prawej stronie. Sprawdź, że komenda:
>> X = B/A
rozwiązuje to równanie macierzowe. Analogicznie, dla przykładu:
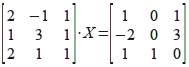
utwórz macierze A (lewa strona) i B (prawa strona) i sprawdź, że przykład ten można rozwiązać za pomocą komendy:
>> X = A\B % nie pomyl kierunku ukośnika! To najczęstszy błąd w takim zadaniu!
Warto tutaj zauważyć, że ukośnik pochyla się w kierunku macierzy A-1.
Odpowiedź
% przykład z macierzami 2x2
>> A = [3 -2; 5 4];
>> B = [-1 2; -5 6];
>> X = B/A
% przykład z macierzami 3x3
>> A = [2 -1 1; 1 3 1; 2 1 1];
>> B = [1 0 1; -2 0 3; 1 1 0];
>> X = A\B
Zadanie (11)
Dany układ równań rozwiąż na dwa sposoby:
a) traktując go jako równanie macierzowe i wykorzystując technikę z ćwiczenia 2.
b) nadal traktując go jako równanie macierzowe – pomnóż macierz B z odpowiedniej strony przez odwrotność macierzy A (wskazówka: polecenie inv).
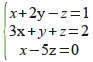
Wykonaj to ćwiczenie (wyniki nie będą poprawne – dlaczego?) ponownie dla przykładu
![]()
Odpowiedź
% Przykład 1:
>> A=[1 2 -1; 3 1 1 ; 1 0 -5]
>> B=[1 2 0]'
>> X=A\B
>> X=inv(A)*B
% Przykład 2:
>> A=[1 -2 5; 2 -1 1]
>> B=[0 1]'
>> X=A\B
>> X=inv(A)*B
Problem polega na tym, że macierz A nie jest kwadratowa! Dostaniemy tylko jedną z nieskończenie wielu odpowiedzi.