Formalna definicja pochodnej
Formalna definicja pochodnej
![]() Wzór na pochodną / Definicja
Wzór na pochodną / Definicja
Pochodną funkcji w punkcie \(x\) liczymy ze wzoru
\(f'(x)=\lim\limits_{\Delta x\rightarrow 0}\frac{\Delta f}{\Delta x}=\lim\limits_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}\)
![]() Ilustracja graficzna
Ilustracja graficzna
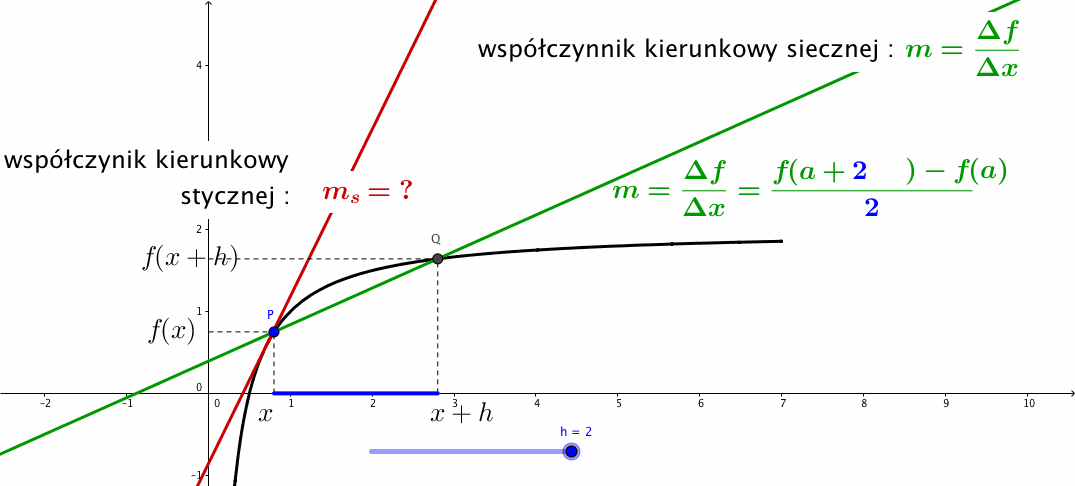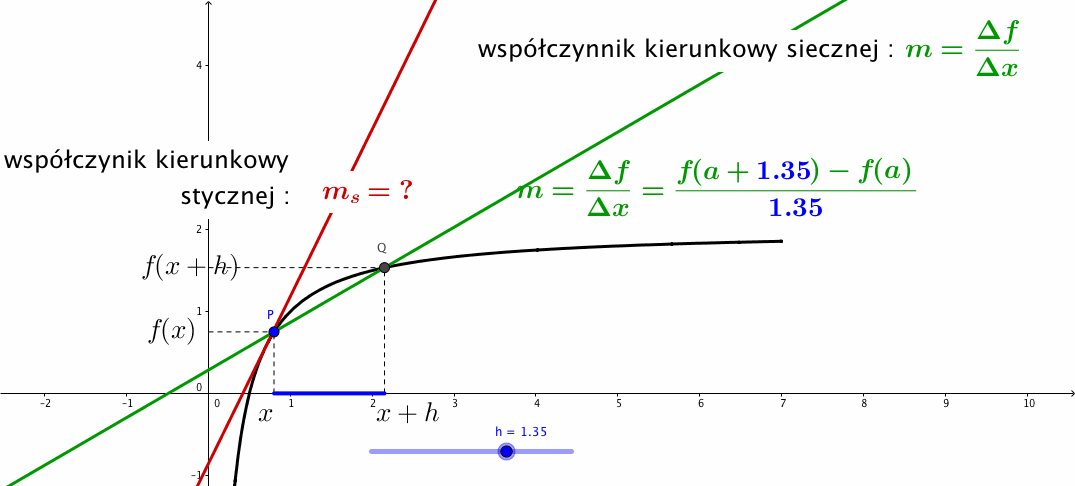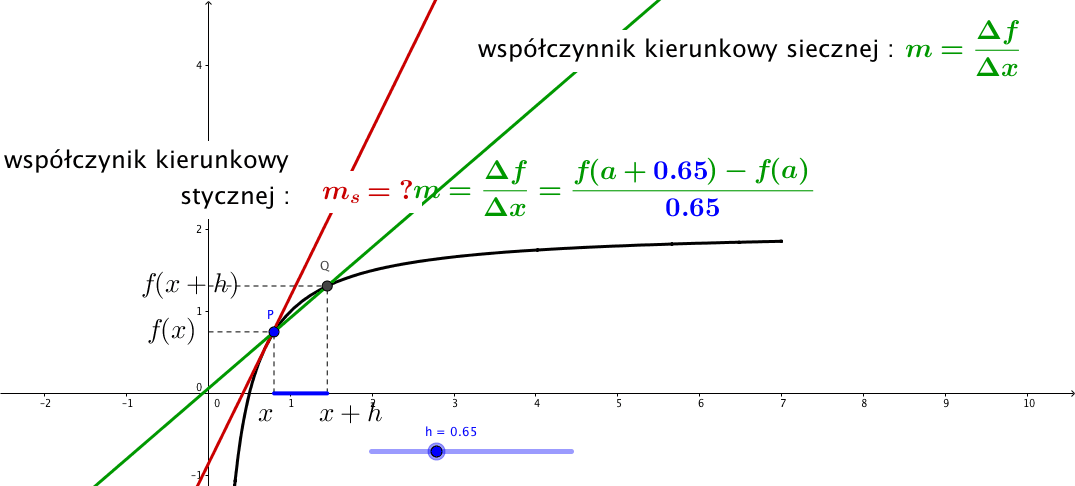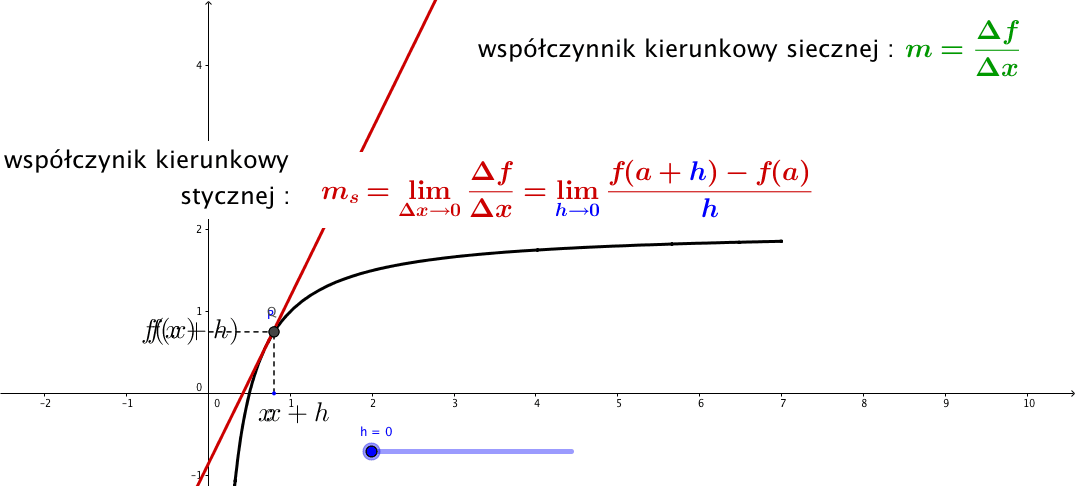
![]() Jeszcze jeden przykład
Jeszcze jeden przykład
Znajdźmy z definicji wzór na pochodną funkcji \(f(x)=x^3\)
\(\frac{\Delta f}{\Delta x}=\frac{f(x+h)-f(x)}{h}=\)
\(=\frac{(x+h)^3-x^3}{h}=\)
\(=\frac{x^3+3x^2h+3xh^2+h^3-x^3}{h}=\)
\(=\frac{h(3x^2+3xh+h^2)}{h}=\)
\(=3x^2+3hx+h^2\;\longrightarrow 3x^2\)
\(\frac{\Delta f}{\Delta x}=\frac{f(x+h)-f(x)}{h}=\)
\(=\frac{(x+h)^3-x^3}{h}=\)
\(=\frac{x^3+3x^2h+3xh^2+h^3-x^3}{h}=\)
\(=\frac{h(3x^2+3xh+h^2)}{h}=\)
\(=3x^2+3hx+h^2\;\longrightarrow 3x^2\)
Last modified: Tuesday, 13.02.2018, 16:56