Pochodne funkcji uwikłanych
Pochodne funkcji uwikłanych
Funkcje uwikłane
Do tej pory mieliśmy do czynienia z funkcjami danymi w sposób jawny, czyli w postaci \(y=f(x)\) . Często jednak zależności między dwiema zmiennymi są podane w sposób uwikłany, \(F(x,y)=0\). Najczęściej też, w takich równaniach chowa się więcej niż jedna funkcja.
W równaniu okręgu \(x^2+y^2=1\) kryją się równania dwóch funkcji
|
\(y=\textcolor{blue}{f_1(x)=\sqrt{1-x^2}}\) \(y=\textcolor{red}{f_2(x)=-\sqrt{1-x^2}}\) |
 |
Często nie jesteśmy w stanie "odzyskać" jawnych wzorów na funkcje z równań uwikłanych. Na przykład w równaniu \(x+y^3-xy=1\) chowają się aż trzy funkcje, ale rozwiązanie tego równaniu ze względu na \(y\) stanowi spore wyzwanie.
|
- górna częśc paraboli \(y=\textcolor{blue}{f_1(x)}\) - dolna część paraboli \(y=\textcolor{red}{f_2(x)}\) - prosta \(y=\textcolor{green}{f_3(x)}\) |
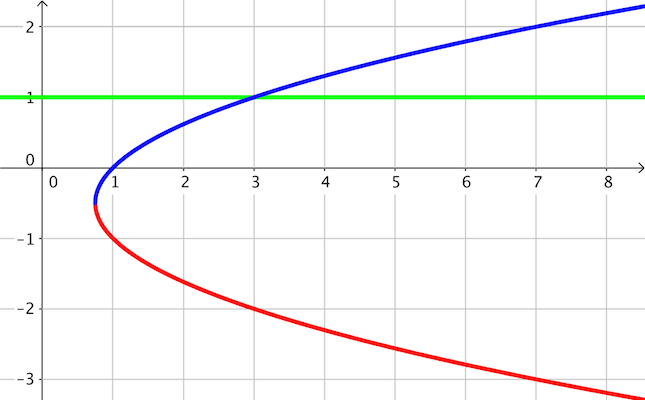 |
Różniczkowanie funkcji uwikłanych
W różniczkowaniu funkcji uwikłanych najważniejszą rzeczą, o której należy pamiętać jest to, że pod literą \(y\) kryje się funkcja \(y(x)\) , więc najczęściej będziemy mieć do czynienia z pochodną funkcji złożonej.
Na przykład, \(\left(y^3\right)' = 3y^2\cdot y'\) , bo tutaj mamy \(\frac{d\left[y(\;)\right]}{d(\;)}\cdot\frac{d\left[(\;)^3\right]}{d(\;)}=\frac{d(y(x))}{dx}\cdot\frac{d\left[(y)^3\right]}{d(y)}\) .
Inny przykład to \(\left(\sqrt{y}\right)'=\frac{1}{2\sqrt{y}}\cdot y'\), bo tu znowu mamy funkcję złożoną, gdzie na zewnątrz jest pierwiastek, w środku funkcja \(y(x)\).
Jeszcze inny przykład to \(\left(\frac{1}{y}\right)'=-\frac{1}{y^2}\cdot y'\), bo tu zewnętrzną funkcją jest \(\frac{1}{(\;)}\) , a w środku znowu jest funkcja \(y(x)\).
Obliczmy pochodną \(\frac{dy}{dx}\) ze wzoru na okrąg \(x^2+y^2=1\) .
Aby podkreślić, że \(y\) jest tutaj funkcją \(x\), pomocne będzie jeżeli zamiast \(y\) będziemy pisać \(y(x)\) , czyli
\(x^2+\left(y(x)\right)^2 = 1\)
Wówczas drugi wyraz jest funkcją złożoną. Liczymy zatem pochodną obu stron równania
\(\frac{d}{dx}(x^2)+\frac{d}{dx}\left[y(x)^2\right] = \frac{d}{dx}(1)\)
\(2x+2y(x)\cdot y'(x)=0\)
\(y'(x)=\frac{dy}{dx}=-\frac{x}{y}\)
Po co w ogóle mowa o funkcjach uwikłanych ? Bo często wygodniej jest, a nawet jest konieczne obliczenie pochodnej funkcji pomimo, że nie mamy jej jawnego wzoru.
|
Znajdź równanie stycznej do krzywej danej wzorem \(x^2+xy-y^3=7\) w punkcie \((3,2)\). |
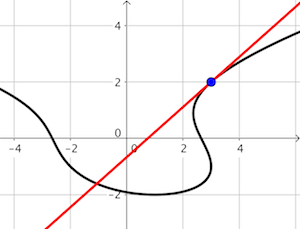 |
Dla przypomnienia, równanie stycznej do krzywej \(y=f(x)\) w punkcie \((x_0,f(x_0))\) dane jest wzorem:
\(y-f(x_0)=f'(x_0)(x-x_0)\)
Aby znaleźć wartość pochodnej, różniczkujemy obie strony równania
\(\frac{d}{dx}(x^2)+\frac{d}{dx}(xy)-\frac{d}{dx}(y^3)=\frac{d}{dx}(7)\)
Trzeci wyraz to pochodna funkcji złożonej, a drugi to iloczyn funkcji, więc pochodną liczymy ze wzoru \((xy)'=(x)'\cdot y + x\cdot(y)'\) ,
\(2x+y+xy'-3y^2y'=0\)
\(y'=\frac{2x+y}{3y^2-x}\)
W punkcie \((3,2)\) ta pochodna wynosi \(y'=\frac{8}{9}\) , zatem równanie stycznej to
\(y-2=\frac{8}{9}(x-3)\) lub \(y=\frac{8}{9}x-\frac{2}{3}\)