Wprowadzenie

Automaty komórkowe (ang. cellular automata) są modelem fizycznego świata, w którym czas i przestrzeń są dyskretne. Każda komórka automatu może przyjmować skończoną liczbę wartości (stanów). Zostały wymyślone przez von Neumanna pod koniec lat 40tych XX wieku, jego główną motywacją było modelowanie mechanizmów prowadzących do autoreprodukcji biologicznych organizmów.

Postulaty automatów komórkowych są następujące:

- automaty komórkowe bazują na przestrzeni złożonej z komórek (zwykle czworokątna siatka),

- każda komórka ma swój wewnętrzny stan, który może przyjmować kilka wartości,

- komórki (a raczej ich stany) ewoluują w dyskretnych krokach czasowych zgodnie z regułami danego automatu.

Prosty przykład

Przyjmijmy, że przestrzeń jest nieskończoną dwuwymiarową powierzchnią złożoną z małych kwadracików – komórek. Niech c=(i,j) będzie komórką leżącą na przecięciu i-tego rzędu i j-tej kolumny. Niech ψ_t(c) będzie stanem komórki c w t-tym kroku czasowym. W tym przykładzie umawiamy się, że funkcja stanu ψ może przyjmować tylko dwie wartości: 0 oraz 1, gdzie 0 oznacza martwą komórkę, a 1 żywą. Wartości ψ₀(c) dla wszystkich komórek c nazywamy konfiguracją początkową, jest ona zwykle zadana przez użytkownika - eksperymentatora lub wybrana losowo przez program komputerowy.

W tym przykładzie zakładamy, że komórka ma 4 sąsiadów – z prawego i lewego boku oraz z góry i z dołu. Jest to tzw. sąsiedztwo von Neumanna. Sąsiedztwo Moore'a zakłada, że oprócz tych czterech sąsiadów komórka ma też sąsiadów po ukosie – metoda ta daje zwykle ciekawsze rezultaty.

Zdefiniujmy funkcję ψ_t(c), którą od teraz będziemy zapisywać jako funkcję ψ_t(i,j), gdyż wygodniej będzie przejść na współrzędne komórki:

• dla t=0 i dowolnego (i,j) funkcja ψ_t(i,j) przyjmuje wartości zadane przez użytkownika

• dla t>0 i dowolnego (i,j):

            ψ_t(i,j) = ( ψ_t-1(i-1,j) + ψ_t-1(i+1,j) + ψ_t-1(i,j-1) + ψ_t-1(i,j+1) ) modulo 2

Inaczej mówiąc, jeżeli komórka ma parzystą liczbę żywych sąsiadów, to w następnej chwili będzie martwa. W przeciwnym razie, będzie żywa.

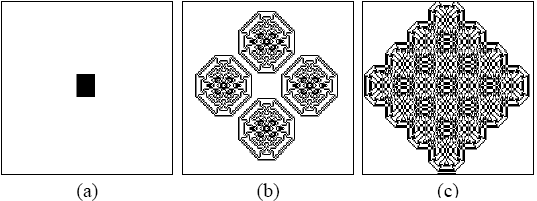
Poniższy rysunek przedstawia działanie tej reguły.

(a) – początkowa konfiguracja,

(b) – konfiguracja po 93 krokach czasowych,

(c) – konfiguracja po 110 krokach czasowych.

Poniższy film pokazuje cykl życia początkowej formy życia (kwadrat 3x3):